Datasets:

ChenLiu1996
/

Brainteaser

Tasks:

Question Answering

Languages:

English

Size:

100K<n<1M

ArXiv:

License:

Dataset card Data Studio Files Files and versions Community

Dataset Preview

Split (1)

train

The full dataset viewer is not available (click to read why). Only showing a preview of the rows.

The dataset generation failed because of a cast error

Error code:   DatasetGenerationCastError
Exception:    DatasetGenerationCastError
Message:      An error occurred while generating the dataset

All the data files must have the same columns, but at some point there are 7 new columns ({'FInal Answers(s)', '185', 'Brute Force (DONT USE)', 'auto bruteforce', 'Open-ended;\nMultiple Final Answers? Y/N', 'auto categories (DONT USE)', 'auto categories (o4mini) (DONT USE)'}) and 8 missing columns ({'Width', 'log10 State Space', '# of clues', 'Secondary category', 'Final answer (deprecated, use full solution)', 'Answer flag', 'Depth', 'ID'}).

This happened while the csv dataset builder was generating data using

hf://datasets/ChenLiu1996/Brainteaser/braingle_Math_with_categories.csv (at revision abd14dc0ecf410c79a0d6847c28cff6c6217d661)

Please either edit the data files to have matching columns, or separate them into different configurations (see docs at https://hf.co/docs/hub/datasets-manual-configuration#multiple-configurations)
Traceback:    Traceback (most recent call last):
                File "/src/services/worker/.venv/lib/python3.9/site-packages/datasets/builder.py", line 1871, in _prepare_split_single
                  writer.write_table(table)
                File "/src/services/worker/.venv/lib/python3.9/site-packages/datasets/arrow_writer.py", line 643, in write_table
                  pa_table = table_cast(pa_table, self._schema)
                File "/src/services/worker/.venv/lib/python3.9/site-packages/datasets/table.py", line 2293, in table_cast
                  return cast_table_to_schema(table, schema)
                File "/src/services/worker/.venv/lib/python3.9/site-packages/datasets/table.py", line 2241, in cast_table_to_schema
                  raise CastError(
              datasets.table.CastError: Couldn't cast
              Title: string
              Question: string
              Answer: string
              Hint: string
              Popularity/Fun: double
              Difficulty: double
              categories: string
              FInal Answers(s): string
              Open-ended;
              Multiple Final Answers? Y/N: string
              Low quality? 
              If low quality, add brief reason
              otherwise leave empty: double
              auto bruteforce: int64
              Brute Force (DONT USE): double
              auto categories (DONT USE): string
              auto categories (o4mini) (DONT USE): string
              185: int64
              -- schema metadata --
              pandas: '{"index_columns": [{"kind": "range", "name": null, "start": 0, "' + 2327
              to
              {'ID': Value(dtype='int64', id=None), 'Title': Value(dtype='string', id=None), 'Question': Value(dtype='string', id=None), 'Answer': Value(dtype='string', id=None), 'Hint': Value(dtype='string', id=None), 'Popularity/Fun': Value(dtype='float64', id=None), 'Difficulty': Value(dtype='float64', id=None), 'categories': Value(dtype='string', id=None), 'Answer flag': Value(dtype='string', id=None), 'Depth': Value(dtype='string', id=None), 'Width': Value(dtype='string', id=None), 'log10 State Space': Value(dtype='string', id=None), '# of clues': Value(dtype='string', id=None), 'Secondary category': Value(dtype='string', id=None), 'Low quality? \nIf low quality, add brief reason\notherwise leave empty': Value(dtype='string', id=None), 'Final answer (deprecated, use full solution)': Value(dtype='string', id=None)}
              because column names don't match
              
              During handling of the above exception, another exception occurred:
              
              Traceback (most recent call last):
                File "/src/services/worker/src/worker/job_runners/config/parquet_and_info.py", line 1433, in compute_config_parquet_and_info_response
                  parquet_operations = convert_to_parquet(builder)
                File "/src/services/worker/src/worker/job_runners/config/parquet_and_info.py", line 1050, in convert_to_parquet
                  builder.download_and_prepare(
                File "/src/services/worker/.venv/lib/python3.9/site-packages/datasets/builder.py", line 925, in download_and_prepare
                  self._download_and_prepare(
                File "/src/services/worker/.venv/lib/python3.9/site-packages/datasets/builder.py", line 1001, in _download_and_prepare
                  self._prepare_split(split_generator, **prepare_split_kwargs)
                File "/src/services/worker/.venv/lib/python3.9/site-packages/datasets/builder.py", line 1742, in _prepare_split
                  for job_id, done, content in self._prepare_split_single(
                File "/src/services/worker/.venv/lib/python3.9/site-packages/datasets/builder.py", line 1873, in _prepare_split_single
                  raise DatasetGenerationCastError.from_cast_error(
              datasets.exceptions.DatasetGenerationCastError: An error occurred while generating the dataset
              
              All the data files must have the same columns, but at some point there are 7 new columns ({'FInal Answers(s)', '185', 'Brute Force (DONT USE)', 'auto bruteforce', 'Open-ended;\nMultiple Final Answers? Y/N', 'auto categories (DONT USE)', 'auto categories (o4mini) (DONT USE)'}) and 8 missing columns ({'Width', 'log10 State Space', '# of clues', 'Secondary category', 'Final answer (deprecated, use full solution)', 'Answer flag', 'Depth', 'ID'}).
              
              This happened while the csv dataset builder was generating data using
              
              hf://datasets/ChenLiu1996/Brainteaser/braingle_Math_with_categories.csv (at revision abd14dc0ecf410c79a0d6847c28cff6c6217d661)
              
              Please either edit the data files to have matching columns, or separate them into different configurations (see docs at https://hf.co/docs/hub/datasets-manual-configuration#multiple-configurations)

Need help to make the dataset viewer work? Make sure to review how to configure the dataset viewer, and open a discussion for direct support.

ID int64	Title string	Question string	Answer string	Hint string	Popularity/Fun float64	Difficulty float64	categories string	Answer flag string	Depth string	Width string	log10 State Space string	# of clues string	Secondary category string	Low quality? If low quality, add brief reason otherwise leave empty null	Final answer (deprecated, use full solution) string
0	Home For Christmas	It was good to have the house full of people again; it had been far too quiet since the last of his seven daughters had left for college--seven daughters with seven different majors at seven different schools. About the only thing they had in common was that they were each dating an athlete, although none of them played the same sport--one was even on his school's fencing team. He was surprised all the boyfriends had come for Christmas dinner, but he supposed that since he was picking up the tab for the airfare, that a free trip to Hawaii in the winter had something to do with it. Each of his first three daughters had gone to Ivy League schools--one even to his alma mater at Harvard; his next two ended up at the University of California, at Los Angeles and Berkeley; and his two youngest got accepted to schools abroad--the University of Tokyo had been a bit of a surprise. Next year, after seven straight years--and for the first time this millennium--he wouldn't be attending a high-school graduation. "Honey, we're ready to eat. Can you get Hank, Ian, James and Kyle? They're in the backyard playing football. The other boys wanted to test themselves against the star quarterback," his wife called from the dining room. The math major said, "I'll get them Dad!" As everyone filed into the dining room, the oldest sister was rehashing the whose-school-and-major-is-better argument with her younger sister about whether Yale or Princeton was a better school and whether history or philosophy was a more useful major. The argument was practically a Christmas tradition by now. The table was arranged with the parents at the two ends and each of the couples seated across from each other with boys seated next to girls along each side. As usual, Angelina and Danica were sitting next to their parents. Curiously, all the athletes that used a ball in their sport were sitting on the same side of the table. Christie, Electra and Edward took their seats first. Once everyone was seated the youngest coyly observed, "I see the biologist is sitting between the two fighters but I'm sitting between the two best passers at the table." "You'd better not make any passes yourself!" Farrah icily replied. She hadn't forgiven her sister for stealing her boyfriend when they were in high school and was not happy to see her seated next to her boyfriend now. "Lighten up, Farrah" the biology major joked. "He wasn't even that cute." "He was adorable!" the youngest interjected. "Everyone's entitled to their opinion," said Brooke. "Let's eat!" The daughter in the middle seat stood up and said, "We have an announcement to make!" After a dramatic pause she screamed "we're getting married!" and flashed the new diamond ring on her finger. The youngest sister squealed with delight at the news. Her fiance joked to his future mother-in-law, "I think she said yes just so she can wear the monogrammed sweater you gave me for Christmas." The baseball player next to her asked her fiance, "Wow, what'd that rock set you back?" "This calls for a toast!" roared Dad. "Oh Honey, that's wonderful news!" Mom gushed. "I just happen to have some champagne right here. Lars, I know you don't drink alcohol, but would you mind pouring some champagne for Gabrielle next to you?" the mother asked, handing the bottle to Lars on her left. "Gabrielle, please pass the bottle around," she asked and then quickly added, "But no alcohol for my three babies, or anyone under 21 for that matter. Honey, there's a store downtown that's having a sale on wedding dresses. Will you have time to go look at some wedding dresses before you leave?" "Sure Mom," her daughter answered. "We have a late flight out, so I can do that on the day we leave." "Michael and I are celebrating New Years Eve at the Sheraton, Waikiki," one of the girls announced. "What a coincidence," said the boy sitting next to her. "We're celebrating New Years at the Sheraton, Los Angeles. It's within walking distance of our apartment so we won't have to worry if we drink too much." "That sounds like a better plan than we have. Somehow, just because my car holds a lot of people, I got roped into being the designated driver for the team" Danica said, looking pointedly at her boyfriend, who gestured to the boy from Princeton saying, "he gave me the idea!" "Girls, your grandmother will be here on Sunday," the father announced. "She'd really like to see you all." "Sorry Dad," the business major replied, "we have to leave tomorrow. There's a huge storm predicted to hit the Eastern United States this weekend and we need to get home before they close the airports. I noticed that each couple is leaving on a different day for six days after we leave." "Sir, we're leaving before Sunday also, so we won't be able to make it either. I'm just glad we don't have to deal with that storm" said the wrestler. The swimmer and water polo player announced their travel plans. One of them remarked that even though his girlfriend and he were departing for Oxford University two days earlier, both couples would get home on the same day. The physics major said "I'll be here to see grandma, but unfortunately we're heading back to California before you go look at the wedding gowns." "Well I'm glad you'll at least be here to see your grandma, but I wish you could stay longer" the dad said. "You know you're my favorite since you were my first to major in a physical science like me," he joked. "I have a tee time at the club on Monday, it's too bad you won't be here," the father remarked to the golfer. "Kyle's got a game next week but you don't," he said to the history major's boyfriend. "How about you join me on the links?" "Sure!" the boyfriend replied enthusiastically. "Since we're leaving the day after him, if you've got room for two more Dad, we just happened to bring our clubs" the second oldest said, winking at her boyfriend. "It's a foursome then!" her dad said happily. Ian grumbled, "Hank you lucky dog, I've wanted to play that course for years!" The boyfriend of the political science major laughed, "I'd like to play there also, but Ian, at least I won't have to travel as far as you to get another opportunity." --------- Identify the boyfriend and his sport, the school, and major for each daughter. Name the order that the daughters were born in and the day of the week that they leave to go home. What is the seating arrangement at the dinner table? Bonus question: what year is it?	From oldest to youngest the sisters are: Who, Boyfriend, Sport, Major, School, Departure day ---------------------------------------------------------- Danica, Hank, Water Polo, History, Yale, Tue Electra, Edward, Fencing, Philosophy, Princeton, Wed Angelina, Lars, Golf, Business, Harvard, Fri Gabrielle, James, Wrestling, Poly Sci., UCLA, Sat Farrah, Kyle, Football, Physics, Berkeley, Mon. Brooke, Michael, Baseball, Biology, Tokyo, Thu Christie, Ian, Swimming, Math, Oxford, Sun The seating arrangement is: ---------- Dad ---------- Hank.............Danica Christie..........Ian Kyle..............Farrah Electra...........Edward Michael..........Brooke Gabrielle........James Lars..............Angelina ---------- Mom ---------- The year is 2003. This is the only year from 2000 to 2007 where Christmas is on a Thursday.	Pay attention to the flow of the conversation, but don't assume more than can be firmly established. Also, some information relies on the following facts: Christmas is on December 25th. New Years Eve is celebrated (usually by drinking too much alcohol) on December 31st. Swimming, fencing and wrestling are not games. Football, baseball, water polo and golf are games played with a ball. Fencing and wrestling are combat competitions. The game of American football is not a collegiate sport outside the United States; the player that passes the ball is the quarterback; there are more than forty players on a football team. Water polo is a game played in a pool with 7 players on each team; points are scored by throwing the ball into the opponents net, which is guarded by the goal keeper; the ball is moved across the pool either by swimming with it or passing it to another player. Ivy League schools are located on the East Coast of the United States. Harvard, Yale and Princeton are all Ivy League schools. Oxford University is in Oxford, England. Tokyo University is in Tokyo, Japan. Los Angeles and Berkeley are cities in California. Waikiki is a city in Hawaii. Hawaii is in the Pacific Ocean. The following are approximate distances from Hawaii: Berkeley and Los Angeles ~ 2500 miles Tokyo ~3900 miles Yale, Harvard and Princeton ~5000 miles England ~7000 miles Biology and physics are physical sciences; none of the other majors is a physical science. High school in America typically includes the last three or four years of school before college. A designated driver remains sober in order to drive people who've had too much alcohol home. A monogram is formed from the first letter of a person's first, last and (sometimes) middle names.	2.73	3.38	2D	F	8	7	29.4526	33	null	null	From oldest to youngest the sisters are: Who, Boyfriend, Sport, Major, School, Departure day ---------------------------------------------------------- Danica, Hank, Water Polo, History, Yale, Tue Electra, Edward, Fencing, Philosophy, Princeton, Wed Angelina, Lars, Golf, Business, Harvard, Fri Gabrielle, James, Wrestling, Poly Sci., UCLA, Sat Farrah, Kyle, Football, Physics, Berkeley, Mon. Brooke, Michael, Baseball, Biology, Tokyo, Thu Christie, Ian, Swimming, Math, Oxford, Sun The seating arrangement is: ---------- Dad ---------- Hank.............Danica Christie..........Ian Kyle..............Farrah Electra...........Edward Michael..........Brooke Gabrielle........James Lars..............Angelina ---------- Mom ---------- The year is 2003. This is the only year from 2000 to 2007 where Christmas is on a Thursday.
1	Prisoners and 2 Switches - Scenario A	The warden meets with 23 new prisoners when they arrive. He tells them, "You may meet today and plan a strategy. But after today, you will be in isolated cells and will have no communication with one another. "In the prison there is a switch room which contains two light switches labeled A and B, each of which can be in either the 'on' or the 'off' position. BOTH SWITCHES ARE IN THEIR OFF POSITIONS NOW.* The switches are not connected to anything. "After today, from time to time whenever I feel so inclined, I will select one prisoner at random and escort him to the switch room. This prisoner will select one of the two switches and reverse its position. He must move one, but only one of the switches. He can't move both but he can't move none either. Then he'll be led back to his cell." "No one else will enter the switch room until I lead the next prisoner there, and he'll be instructed to do the same thing. I'm going to choose prisoners at random. I may choose the same guy three times in a row, or I may jump around and come back." "But, given enough time, everyone will eventually visit the switch room as many times as everyone else. At any time any one of you may declare to me, 'We have all visited the switch room.' "If it is true, then you will all be set free. If it is false, and somebody has not yet visited the switch room, you will be fed to the alligators." *note - the only difference from Scenario B, the original position of the 2 switches are known.	1. Appoint a "scorekeeper" and the other 22 prisoners as "transmitters". 2. When a transmitter enter the switch room for the first time, he will flick switch B ON if he sees it in the OFF position. Alternatively, he will flick switch A if he sees switch B is in the ON position and waits for his next visit. The transmitter's mission is to find ONE opportunity to flick switch B to the ON position. After he completes his mission, he will flick switch A for all subsequent visits. In short, each transmitter's role is to send a signal to the scorekeeper that he has been to the switch room. 3. The scorekeeper's role is to flick off switch B whenever he sees it in the ON position. Each time he flicks off switch B he adds 1 to his score. When he sees switch B is already OFF, he flicks switch A instead and does not add to the score. As soon as he accumulates 22, he reports to the Warden.	Assuming that: A) There is no restriction on the amount of time the prisoners could take before sending the notice to the warden that everyone has been to the switch room at least once. B) There is no restriction on the number of time each prisoner can visit the switch room C) The warden will not attempt any foul moves, such as intentionally not bringing a certain prisoner to the switch room forever.	2.97	3.23	Algorithm	A	x	x	x	x	Communication	null	1. Appoint a "scorekeeper" and the other 22 prisoners as "transmitters". 2. When a transmitter enter the switch room for the first time, he will flick switch B ON if he sees it in the OFF position. Alternatively, he will flick switch A if he sees switch B is in the ON position and waits for his next visit. The transmitter's mission is to find ONE opportunity to flick switch B to the ON position. After he completes his mission, he will flick switch A for all subsequent visits. In short, each transmitter's role is to send a signal to the scorekeeper that he has been to the switch room. 3. The scorekeeper's role is to flick off switch B whenever he sees it in the ON position. Each time he flicks off switch B he adds 1 to his score. When he sees switch B is already OFF, he flicks switch A instead and does not add to the score. As soon as he accumulates 22, he reports to the Warden.
2	Mystery Number 5	There is a ten-digit mystery number (no leading 0), represented by ABCDEFGHIJ, where each numeral, 0 through 9, is used once. Given the following clues, what is the number? 1) A + B + C + D + E is a multiple of 6. 2) F + G + H + I + J is a multiple of 5. 3) A + C + E + G + I is a multiple of 9. 4) B + D + F + H + J is a multiple of 2. 5) AB is a multiple of 3. 6) CD is a multiple of 4. 7) EF is a multiple of 7. 8) GH is a multiple of 8. 9) IJ is a multiple of 10. 10) FE, HC, and JA are all prime numbers.	5736912480 A = 5, B = 7, C = 3, D = 6, E = 9, F = 1, G = 2, H = 4, I = 8, J = 0 1) 5 + 7 + 3 + 6 + 9 = 30, which is a multiple of 6. 2) 1 + 2 + 4 + 8 + 0 = 15, which is a multiple of 5. 3) 5 + 3 + 9 + 2 + 8 = 27, which is a multiple of 9. 4) 7 + 6 + 1 + 4 + 0 = 18, which is a multiple of 2. 5) 57 is a multiple of 3. 6) 36 is a multiple of 4. 7) 91 is a multiple of 7. 8) 24 is a multiple of 8. 9) 80 is a multiple of 10. 10) 19, 43, and 05 are prime numbers. A) The sum of digits 0 through 9 is 45. To satisfy Conditions 1 and 2, a pair of multiples must equal 45. The only pair that satisfies those conditions are 30 (multiple of 6) and 15 (multiple of 5). Likewise, to satisfy Conditions 3 and 4, the pair of multiples must be 27 (multiple of 9) and 18 (multiple of 2). B) Make lists of the multiples of 3, 4, 7, 8, and 10 (for Conditions 5 through 9). Delete multiples whose digits are the same (33, 44, 66, 77, 88, 99). C) To satisfy Condition 9, J must be 0. Delete multiples that require 0 in a different location. For JA to be prime (Condition 10), A must be: 2, 3, 5, or 7. Delete multiples of 3 that have another digit for A. D) For FE and HC to be prime (Condition 10), C and E can not be even or 5. Delete multiples of 4 and 7 that have another digit for C and E. E) Per Condition 4, B + D + F + H + J = 18. D, H, and J must be even (required to form multiples of even numbers). To attain the sum of 18 (an even number), B and F must either be both odd or both even. If both are even, then the sum of those five digits would be 20. B and F must be odd. Delete multiples of 3 and 7 that have an even digit for B and F. The only remaining multiple of 7 is 91. E is 9 and F is 1. Delete multiples that require 1 or 9 in a different location. F) The only remaining options for AB contain 7. Delete multiples that require 7 in a different location. The only remaining options for CD contain 3. Delete multiples that require 3 in a different location. G) To satisfy Condition 1, CD must be 36 and AB must be either 57 or 75. C is 3 and D is 6. Delete multiples that require 5, 6, or 7 in a different location. H) The only remaining options for GH contain 4. Delete multiples that require 4 in a different location. I) Per Condition 3, A + C + E + G + I = 27. Since C =3 and I = 9, the other three must total 15. There is only one combination of remaining multiples (57, 24, and 80) that can satisfy this condition. A is 5, G is 2, and I is 8. B is 7 and H is 4.	Notice that when combining clues 1 and 2, you have information about the sum of digits. You can do the same for clues 3 and 4.	2.06	3.22	Number	F	2	10	6.51401	10	null	null	5736912480
3	Mystery Number 7	There is a ten-digit mystery number (no leading 0), represented by ABCDEFGHIJ, where each numeral, 0 through 9, is used once. Given the following clues, what is the number? 1) Either A = B / 3 or A = G + 3. 2) Either B = I - 4 or B = E + 4. 3) Either C = J + 2 or C = F * 3. 4) Either D = G * 4 or D = E / 3. 5) Either E = J - 1 or E = D / 4. 6) Either F = B * 2 or F = A - 4. 7) Either G = F + 1 or G = I - 3. 8) Either H = A / 2 or H = C * 3. 9) Either I = H + 3 or I = D / 2. 10) Either J = H - 2 or J = C * 2.	5038612947 A = 5, B = 0, C = 3, D = 8, E = 6, F = 1, G = 2, H = 9, I = 4, J = 7 1) A = G + 3 = 2 + 3 = 5. 2) B = I - 4 = 4 - 4 = 0. 3) C = F * 3 = 1 * 3 = 3. 4) D = G * 4 = 2 * 4 = 8. 5) E = J - 1 = 7 - 1 = 6. 6) F = A - 4 = 5 - 4 = 1. 7) G = F + 1 = 1 + 1 = 2. 8) H = C * 3 = 3 * 3 = 9. 9) I = D / 2 = 8 / 2 = 4. 10) J = H - 2 = 9 - 2 = 7. A) Check each letter for any value that it can not be on the left side of an equation. For example, A can not be 0, as B would also have to be 0 or G would have to be negative. On the first pass through the letters, the following can be determined: A not 0, C not 0, C not 1, D not 0, D not 5, D not 6, D not 7, D not 9, E not 9, F not 7, F not 9, G not 8 (because F not 7), H not 0, H not 5, H not 7, H not 8, I not 0, I not 3 (because H not 0 and D not 6), I not 8 (because H not 5), J not 3 (because H not 5), J not 5 (because H not 7), and J not 9. B) Make a second pass through the letters. The following can be determined: C not 5, C not 7, D not 3, E not 4, E not 8, and G not 0. C) Make a third pass. The following can be determined: B not 8. D) For D, only four numbers are still valid: 1, 2, 4, and 8. Plug each of these numbers into D and check the resulting flow of equations. If D = 1, then the resulting flow will lead to J having to be both 4 and 0. If D = 2, then the resulting flow will lead to 2 also being assigned to G. If D = 4, then the resulting flow will lead to 4 also being assigned to either A or I. If D = 8, then G = 2, F = 1, and A = 5. E) For E, four numbers are still valid: 0, 3, 6, and 7. Plug each number into E and check the resulting flow. If E = 0, then the flow will lead to J being assigned 1, which has already been assigned to F. If E = 3, then the flow will lead to C being assigned 2, which has already been assigned to G. If E = 7, then the flow will lead to J being assigned 8, which has already been assigned to D. If E = 6, then J = 7, H = 9, and C = 3. F) The only remaining value for I is 4, which leaves 0 being assigned to B.	Check each letter for any value that it can not be on the left side of an equation. For example, A can not be 0, as B would also have to be 0 or G would have to be negative.	2.45	3.21	Compound	F	2	10	6.51401	10	Number	null	5038612947
4	1000 Point Star	Typical "stars" are drawn in connected, but not repeated, line segments. For example, a 5-point star is drawn as such - line segments AC, CE, EB, BD, DA. The segments must always alternate a constant number of points (in the above case, skipping 1 point in between). Given the information that there is only 1 way to draw a 5-point star, and that there is NO way to draw a 6-point star (in continuous lines, that is), and there are 2 ways to draw a 7-point star, how many different ways are there to draw a 1000-point star?	199. First, let's examine the 5-point star and why there is only that one, described, way to draw it. Starting at A, you cannot go straight to point B, otherwise you will have a pentagon, not a star. Same with point E. AC and AD (and their progressions) yield identical pictures (notice that the last segment in the AC one is DA, literally reverse all the letters to get AD ending in CA). Now, for a 6-point star, there are points A, B, C, D, E, and F. Starting at A, we cannot go to B or F, because then we have a hexagon. If we go AC, then we must go CE, then CA... making a triangle, not a 6-point star. Going backwards, AE, EC, EA; mirror image. If we skip 2 points, we go AD, then DA, a straight line, hardly a 6-point star. For a 7-point star, A-G, AB and AG are not possible, as that's a heptagon. AC, CE, EG, GB, BD, DF, FA is one way to draw the star, skipping one point in between. Also, AD, DG, GC, CF, FB, BE, EA, skipping two points in between each, is the other way. The last two line possibilities, AF and AE are mirror images of the two working scenarios. Examining the above information a little more deeply, we see that we must divide all possible drawings by two, to get rid of the mirror images. Also, we cannot use the point immediately to the left, that is AB as a segment. This explains why there is only 1 way for a 5-point, and 2 for a 7-point, but does not explain the 6-point. Of those remaining points (dealing only with the first half, again, mirror images), those that are factors of the number of total points do not work, because you will end up back at the starting point before hitting every number. AC is a factor in six because it passes point B, so it's 2. AD is a factor of 3 (B, C and D). Not only factors, but multiples of factors, as well (for example, skipping 4 points in the 6-point still does not work). Using the knowledge of mirrors, first point impossibility (AB) and factors, we see that the number 1000 is made up of 10^3, or 2^35^3. Without going through every factor, it's quickly and easily discernible that of the numbers 1-1000, 2 or multiples of it encompass 500 numbers, all evens. Any multiple of 5 includes 200 numbers, half of which end in 0 and are already included with the 2's, so there are 600 unique factors and multiples between 1 and 1000. That leaves us with 400 that are not*, which should explain how many unique stars we can make. Remember to cut it in half because of mirroring, leaving us with 200, and to discount the AB segment (factor of 1), leaving us with 199. (If you discount AB, and THEN halve it, remember you needed to remove A[Z], the mirror image of that point).	It's not guess work. Think of factors and mirror images. Try drawing out examples.	2.15	3.19	Math	F	x	x	x	x	null	null	199
5	Five Cards	I was playing a game of five card draw poker with a bunch of logicians. By the time we had finished bidding and were just about to reveal our cards, I was pretty confident I would win of the four of us remaining. I had three nines, some face card (I can't remember what suit or even whether it was a jack, queen, or king) and a four. (Or was it a five? I can't remember.) I was even more sure when two of my opponents laid down their cards. One had a pair of fours and a pair of sevens, the other had a pair of twos and a pair of eights. My third opponent, however, laid down his five cards face down in a row. He said, "I have a straight, and the cards are, from lowest to highest: a ten, a jack, a queen, a king, and an ace. I have at least one card of each of the four suits: clubs, spades, hearts, and diamonds. I am fairly certain that this is the winning hand, but I'm feeling generous today, and I will give a third of the pot to whoever can determine which suit I have two cards of. Now I know you can't figure it out without some clues. Here they are: 1. The king is next to at least one diamond. 2. The queen is next to exactly one heart. 3. The jack is next to at least one spade, but is not next to any hearts. 4. The ten is next to at least one club. 5. The ace does not border any black cards, nor does it border any diamonds. 6. My two cards of the same suit are not next to each other. 7. Of the ten possible pairings of cards, only one pair, when removed, leaves three cards in ascending order from left to right. 8. My ace is not the card on the far left." There was a minute's silence. One of the other logicians said, "I give up! There's no way to figure that out!" The other agreed. But I didn't. I had just figured out which suit he had two of. Which suit is it?	The two cards on the ends and the card in the middle border a combined number of two suits. So at least one pair of them should be listed as bordering a card of the same suit in clues 1-5. Of the five, only the ace and the queen meet this criterion, so they must be two cards apart. One of them must be in the center, but it can't be the ace (the two cards on the ends would only border hearts - and one of them has to be bordering something else from clues 1-4), so it must be the queen. The ace is not on the left end from clue 8, so it must be on the right end, and the card next to it must be a heart. So far we have this(X represents unknown): X X Q X A X X X H X At least one of the two cards to the left of the queen is lower than the queen (two of the remaining cards are lower, and only one can be right of the queen), so the triplet that is in ascending order is the queen, the ace, and the single card to the left of the queen that is lower than the queen. That means the king is left of the queen, and is also left of both the jack and the ten (otherwise, jack king ace or ten king ace would be a second triplet), so it must be on the far left. The jack must be left of the ten (or else ten jack ace would be a second triplet), so it must be second from the left, and the ten must be second from the right. The only card next to the king is the jack of diamonds (it's a diamond from clue 1). So far we have(T is ten): K J Q T A X D X H X Now we seem to be stuck. We don't have any more clues that can be used. So how did I figure it out? I held a face card (I said so myself in the intro). I must have known it cannot be that card and deduced the correct answer from there. But which card did I have? We already know the suit of the jack, so my holding a jack would not help. Could I have held a queen? No, because I know the queen to either be a spade or club (clue 6), so one of the cards next to the queen would have its clue satisfied (see clues 3 and 4), and I could not determine the suit of the card on the other side of it. Therefore, I must have held a king. But which king? I know the king is not a diamond (clue 6) or a heart (clue 3). If I held the king of clubs, then the king next to the jack would have satisfied the jack's clue, and I could not have determine the suit of either card next to the ten. Therefore, I held the king of spades. The king of clubs must have been on the far left (only suit available), so the only card next to the jack that could be a spade is the queen, so the only card next to the ten that could be a club is the ace. In summary: K J Q T A C D S H C Therefore there are two CLUBS.	The first step is to determine where the ace goes. Also, consider this: How could I have figured it out when two expert logicians couldn't?	2.48	3.18	1D	H	3	5	3.8573	8	null	null	CLUBS
6	World of Nerds	Five friends spend every Monday night eating Chinese food from the Golden Dragon. Howard has Mu Shu Pork, Leonard has Spicy Szechuan Tofu, Penny has Shrimp with Lobster Sauce, Raj has Beef with String Beans, and Sheldon has Chicken and Broccoli: diced, not shredded, with brown rice, not white, low-sodium soy sauce and the good hot mustard from the Korean grocery. After dinner, they play a role-playing game called World of Nerds. In this game, each player takes on a character belonging to a different race of creature, has a different occupation, uses a different sort of weapon, specializes in fighting a particular kind of monster, and has a different skill level. Can you determine the characteristics of each player's character from the following clues before someone sits in Sheldon's spot? Players: Howard, Leonard, Penny, Raj and Sheldon Races: elf, gremlin, halfling, hobbit and ogre Occupations: archbishop, merchant, paladin, sorcerer and thief Weapons: bolo, crossbow, dagger, fireballs and mace Monsters: chimeras, giants, harpies, kobolds and orcs Skill levels: range from 10-32 Clues: 1. The five characters in the game are Penny's, the 24th-level ogre, the thief, the fireball user, and the one skilled at fighting orcs. 2. The paladin isn't an elf. 3. The bolo user has a skill level twice that of the halfling. 4. Raj's character has a skill level eight levels higher than the paladin, who in turn is eight levels higher than the crossbow user. 5. The hobbit is no good at fighting giants. 6. The elf (who doesn't care for crossbows) is ten levels higher than the one who fights kobolds. 7. The one who is adept at fighting chimeras is four levels higher than Leonard's character (who isn't the archbishop). 8. The character at the lowest level (who isn't Penny) is at level ten and uses a dagger. 9. Neither the archbishop nor the merchant belongs to the race of gremlins. 10. The giant fighter never uses a mace in battle. 11. Raj's character isn't the elf. 12. Penny's character doesn't use the crossbow. 13. Howard's character is not particularly adept at fighting harpies.	Howard is the halfling and a level 10 thief who fights kobolds with a dagger. Leonard is the hobbit and a level 16 merchant who fights orcs with a crossbow. Penny is the elf and a level 20 archbishop who fights chimeras with a bolo. Raj is the gremlin and a level 32 sorcerer who fights giants with fireballs. Sheldon is the ogre and a level 24 paladin who fights harpies with a mace. Explanation: The first step is to determine the actual skill levels of the five players. The lowest level is 10, held by the character using a dagger (clue 8). From (4), the character using a crossbow has an unknown level, let's call it x; the paladin has x+8 and Raj has x+16. Note that x must be greater than 10 and less than or equal to 16, or else x+16 would be greater than 32. The elf is none of these four players (2, 11, 6), but has a skill level of 10 more than one of them (6). This could be 20, x+10 or x+18. One skill level has to be 24 (1), two skill levels must have a difference of 4 (7) and one skill level must be twice another (3). If x=11, then the skill levels are 10, 11, 19, 27 and the elf's is either 20, 21 or 29. None of these is 24; therefore, x isn't 11. Similarly x isn't 12, 13 or 15. If x=14, then the skill levels are 10, 14, 22, 30 and the elf's is either 20, 24 or 32. This provides a skill level of 24, but for the elf, instead of the ogre; therefore, x isn't 14. Therefore, x=16 and the skill levels are 10 [dagger], 16 [crossbow], 24 [paladin=ogre], and 32 [Raj]. The elf's skill level must be 20, not 26, in order to satisfy clue (7). This means the elf fights chimeras and Leonard's character uses the crossbow. Now that we know the skill levels, we can start building a list of the players, starting with the first clue: Player 1 = Penny Player 2 = ogre, level 24, paladin Player 3 = thief Player 4 = fireballs Player 5 = orcs Since the elf has a skill level of 20, the kobold fighter is level 10 (6), and uses the dagger (8). Penny's character doesn't use the dagger (8), and neither does the ogre, who is level 24. Therefore the thief does: Player 1 = Penny Player 2 = ogre, level 24, paladin Player 3 = level 10, thief, kobolds, dagger Player 4 = fireballs Player 5 = orcs Neither Penny's character (12) nor the ogre (4) uses the crossbow [Leonard], so the orc fighter must: Player 1 = Penny Player 2 = ogre, level 24, paladin Player 3 = level 10, thief, kobolds, dagger Player 4 = fireballs Player 5 = Leonard, level 16, orcs, crossbow The ogre can't use the bolo, as no one has level 12 (3), so Penny's character uses the bolo and the thief is the halfling. This leaves the ogre using the mace: Player 1 = Penny, bolo Player 2 = ogre, level 24, paladin, mace Player 3 = halfing, level 10, thief, kobolds, dagger Player 4 = fireballs Player 5 = Leonard, level 16, orcs, crossbow This means that Raj's character, at level 32, must use fireballs, and Penny's character must be the level 20 elf who fights chimeras: Player 1 = Penny, elf, level 20, chimeras, bolo Player 2 = ogre, level 24, paladin, mace Player 3 = halfing, level 10, thief, kobolds, dagger Player 4 = Raj, level 32, fireballs Player 5 = Leonard, level 16, orcs, crossbow The ogre, who uses a mace, doesn't fight giants (10); therefore the ogre fights harpies, leaving Raj's character as the giant fighter: Player 1 = Penny, elf, level 20, chimeras, bolo Player 2 = ogre, level 24, paladin, harpies, mace Player 3 = halfing, level 10, thief, kobolds, dagger Player 4 = Raj, level 32, giants, fireballs Player 5 = Leonard, level 16, orcs, crossbow The hobbit doesn't fight giants (5), so the hobbit must fight orcs, leaving Raj as the gremlin. The gremlin isn't the archbishop or the merchant, and so the gremlin is the sorcerer: Player 1 = Penny, elf, level 20, chimeras, bolo Player 2 = ogre, level 24, paladin, harpies, mace Player 3 = halfing, level 10, thief, kobolds, dagger Player 4 = Raj, gremlin, level 32, sorcerer, giants, fireballs Player 5 = Leonard, hobbit, level 16, orcs, crossbow Leonard's character must be the merchant, rather than the archbishop (7), leaving Penny's character as the archbishop: Player 1 = Penny, elf, level 20, archbishop, chimeras, bolo Player 2 = ogre, level 24, paladin, harpies, mace Player 3 = halfing, level 10, thief, kobolds, dagger Player 4 = Raj, gremlin, level 32, sorcerer, giants, fireballs Player 5 = Leonard, hobbit, level 16, merchant, orcs, crossbow Howard's character doesn't fight harpies (13), so that falls to Sheldon's ogre, while Howard's halfling fights kobolds. And that completes the list: Player 1 = Penny, elf, level 20, archbishop, chimeras, bolo Player 2 = Sheldon, ogre, level 24, paladin, harpies, mace Player 3 = Howard, halfing, level 10, thief, kobolds, dagger Player 4 = Raj, gremlin, level 32, sorcerer, giants, fireballs Player 5 = Leonard, hobbit, level 16, merchant, orcs, crossbow	Start by determining the 5 skill levels.	2.92	3.15	0D	F	6	5	10.3959	13	null	null	Penny, elf, level 20, archbishop, chimeras, bolo Sheldon, ogre, level 24, paladin, harpies, mace Howard, halfing, level 10, thief, kobolds, dagger Raj, gremlin, level 32, sorcerer, giants, fireballs Leonard, hobbit, level 16, merchant, orcs, crossbow
7	Divine Deception	Sailing through a thick fog, you come upon a mysterious island shrouded in mist. A towering volcano in the center of the island pierces the clouds, billowing smoke into the sky. You land your boat and set out to ascend the peak. After an arduous climb, you approach the volcano summit, where lava glows red within a vast crater. Here, you are approached by three gods and their herald. Problem On the summit of this remote volcano, the herald proclaims that you have been selected for a trial. He then lays out the rules for you. First, you know that one of the three gods always tells the truth, another always lies, and the third will respond to questions randomly. Therefore, let us call the gods True, False, and Random. Second, the gods speak a different language. They understand all languages perfectly well, but only answer questions with either ja or da, the words for yes and no. You do not know which god is which, and you do not know which word means yes and which word means no. Finally, you have an existential problem on your hands. You may ask three yes-or-no questions, each one directed to only one god, and only that god will answer with either ja or da. If you can determine the identities of the three gods, they will send you on your way with their blessing, and you can be assured of a prosperous and fulfilled life. If you fail to determine the identities of the gods, however, they will be less generous in their treatment. The volcano pit smokes and glows red beside you. With your three questions, how do you figure out which god is True, which is False, and which is Random?	First, ask the god standing in the middle, "If I were to ask you if the god to your left is Random, would you say ja?" By phrasing questions as hypotheticals, you can ask the gods an embedded question. As long as you ask either True or False, the god will respond with the same word you use ("would you say ja?") if the answer to the embedded question is affirmative, and the opposite word if the answer is negative. If the god says ja, then there are two possibilities: either the god to his left is Random, and the god speaking is either True or False; or the god speaking is Random. Either way, you know the god to his right is not Random. Similarly, if the god says da, then there are two possibilities: either the god to his right is Random, and the god speaking is True or False; or the god speaking is Random. In this case, you know the god to the left is not Random. The next step is to approach the god that you know is not Random, and figure out if he is True or False. Because you still do not know the meanings of ja and da, you need to do this by using the same hypothetical structure, asking, "If I were to ask you if you are True, would you say ja?" If the god is True, they will answer ja. If the god is False, they will answer da. (False's response in this case is essentially either: "no I would not say yes," even though he would; or "yes I would say no," even though he wouldn't.) Finally, now that you have identified a god as either True or False, you can use the same question structure one last time to identify the other gods (you need to stick to it because you still don't know the meanings of ja and da). Simply ask, "If I were to ask you if the god in the middle is Random, would you say ja?" If the answer is ja, then the god in the middle is Random, and the third god is either True or False (the opposite of the one you have already identified). If the answer is da, then the god in the middle is True or False, and the third god is Random.	Can you phrase a question so that both True and False have to say the same thing?	2.58	3.12	Algorithm	A	x	x	x	x	Liars	null	First, ask the god standing in the middle, "If I were to ask you if the god to your left is Random, would you say ja?" By phrasing questions as hypotheticals, you can ask the gods an embedded question. As long as you ask either True or False, the god will respond with the same word you use ("would you say ja?") if the answer to the embedded question is affirmative, and the opposite word if the answer is negative. If the god says ja, then there are two possibilities: either the god to his left is Random, and the god speaking is either True or False; or the god speaking is Random. Either way, you know the god to his right is not Random. Similarly, if the god says da, then there are two possibilities: either the god to his right is Random, and the god speaking is True or False; or the god speaking is Random. In this case, you know the god to the left is not Random. The next step is to approach the god that you know is not Random, and figure out if he is True or False. Because you still do not know the meanings of ja and da, you need to do this by using the same hypothetical structure, asking, "If I were to ask you if you are True, would you say ja?" If the god is True, they will answer ja. If the god is False, they will answer da. (False's response in this case is essentially either: "no I would not say yes," even though he would; or "yes I would say no," even though he wouldn't.) Finally, now that you have identified a god as either True or False, you can use the same question structure one last time to identify the other gods (you need to stick to it because you still don't know the meanings of ja and da). Simply ask, "If I were to ask you if the god in the middle is Random, would you say ja?" If the answer is ja, then the god in the middle is Random, and the third god is either True or False (the opposite of the one you have already identified). If the answer is da, then the god in the middle is True or False, and the third god is Random.
8	Mad Ade's Fishing Trip	Mad Ade went on an eight day fly fishing trip around the purple ridged mountains of Madadia and got to fish seven days of it last May. On every day, from May 14 to the 21st, except the 16th, when a severe thunderstorm kept him in his tent, he fished around Madadia. Though he caught many fish--all of which he released--each day, one special fish stood out. Each special fish was of a different variety: Monkey Trout, Brookside Trout, Cut Throat, Dolly Varden, Humpback, Lake Trout, and Rainbow, and a different size: 8 inches, 16 inches, 17 inches, 19 inches, 22 inches, 24 inches, and 27 inches. Every day, Mad Ade tried a different secret fishing spot: Big Little Falls, Bottle Well, Deep Channel, Old Cutbank, Big Rock Isle, Dish Creek, and Little Curl. And each special fish was caught on a different fly that Mad Ade tied himself: a Parachute Adams, an Elk Hair Caddis, a Humpy, a MayFly, Mad Ade's Little Mouse, a Stonefly Nymph, and a Yuk Bug. Three of the flies, Mad Ade's little Mouse, the Yuk Bug, and Stonefly Nymph, were fished as wet flies, the rest were fished as dry flies. 1) Mad Ade caught the smallest of his special fish, a little Brookside, after he caught the fish on his Elk Hair Caddis, but before he caught the fish in Deep Channel. His shiny Dolly Varden was not the fish lured from the depths of Bottle Well. Mad Ade caught either the smallest or his second to largest fish on his third fishing day. 2) Mad Ade caught a fish off Big Rock Isle on the 19th. He fought either the Humpback or the 24 inch monster on the 21st. On the fourth day of his trip, Mad Ade landed a fish over twenty inches long by the Old Cutbank on a wet fly. The fish Mad Ade landed with a net at Little Curl was larger than the one he worked onto shore at Dish Creek, but it was not as large as the one he lifted from the water at Big Little Falls. 3) Mad Ade caught the 24 inch fish on his Little Mouse after he caught the Dolly Varden, but before he hooked a real jumper with his Parachute Adams. Because he preferred dry flies, Mad Ade only used dry flies after using a wet fly on the 19th. Mad Ade used a Mayfly to fish Dish Creek. Mad Ade caught his fish on the Mayfly three calendar days (two fishing days) after he caught a fish with the Stonefly Nymph. 4) Mad Ade's five mile hike, along a mountain trail to Big Little Falls, paid off on his last day with a prized Humpback trout. At least four fishing days passed between the time that Mad Ade used the Stonefly Nymph and his Humpy. The Monkey Trout Mad Ade caught on the 17th was longer than the Rainbow he caught, but smaller than his Lake Trout. 5) The deep hole of Bottle Well yielded Mad Ade a 19 incher on the first or second day of his trip. With one exception, Mad Ade caught fish of even sizes on even number days and fish of odd sizes on odd days. Although they both jumped and splashed over the water the same way, the Rainbow Mad Ade caught was bigger than his Cut Throat.	Mad Ade caught a fish off Big Rock Isle on the 19th (2). The Monkey Trout Mad Ade caught on the 17th (4). Mad Ade caught either the smallest or his second to largest fish on his third fishing day. (1) 17th is 8 or 24. On the fourth day of his trip, Mad Ade landed a fish over twenty inches long by the Old Cutbank on a wet fly. (2) 17th is 24 and Cutbank. Mad Ade caught the 24 inch fish on his Little Mouse (3). With one exception, Mad Ade caught fish of even sizes on even number days and fish of odd sizes on odd days. (5) He fought either the Humpback or the 24 inch monster on the 21st. Humpback is 21st. (2) Mad Ade's five mile hike, along a mountain trail to Big Little Falls, paid off on his last day with a prized Humpback trout. (5) Humpback is Big Little Falls. The deep hole of Bottle Well yielded Mad Ade a 19 incher on the first or second day of his trip. (5) First day is 14th, so 19 incher had to be second day, 15th. 15th then is Bottle. Mad Ade caught the 24 inch fish on his Little Mouse after he caught the Dolly Varden (3). Mouse is 24 inch fish on 17th. Dolly is 14th or 15th. Mad Ade caught his fish on the Mayfly three calendar days (two fishing days) after he caught a fish with the Stonefly nymph. (3) Mayfly can only be 18th, as Mouse is 17th. Stonefly is 15th. Mad Ade used a Mayfly to fish Dish Creek. At least four fishing days passed between the time that Mad Ade used the Stonefly Nymph and his Humpy. (4) Stonefly is 15th, so Humpy is 21st. Mad Ade only used dry flies after using a wet fly on the 19th. (3) Only wet fly left is Yuk Bug, so Yuk Bug is 19th. Mad Ade caught the smallest of his special fish, a little Brookside, after he caught the fish on his Elk Hair Caddis, but before he caught the fish in Deep Channel. (1) Elk Hair Caddis can only be 14th. Parachute Adams, the only fly left, is 20th. His shiny Dolly Varden was not the fish lured from the depths of Bottle Well. Bottle is 15th, so Dolly is 14th. (1) Mad Ade caught the smallest of his special fish, a little Brookside, after he caught the fish on his Elk Hair Caddis, but before he caught the fish in Deep Channel. (1) Brookside, 8 inches, (even) can only be Mayfly or Adams. The fish Mad Ade landed with a net at Little Curl was larger than the one he worked onto shore at Dish Creek, but it was not as large as the one he lifted from the water at Big Little Falls. (2) Adams can only be Little Curl or Deep Channel. It's not Channel (1) and not Little Curl (2), so Brookside is Dish Creek. Mad Ade caught the smallest of his special fish, a little Brookside, after he caught the fish on his Elk Hair Caddis, but before he caught the fish in Deep Channel. (1) So, Deep Channel is 20th, and 14th is Little Curl (last one). The Monkey Trout Mad Ade caught on the 17th was longer than the Rainbow he caught, but smaller than his Lake Trout. (4) 17th is Monkey, 24 inches, so Lake can only be 27. Only odd without a named fish name is 19th. So 19th is Lake Trout and 27 inches. 21st is 17 inches, only odd left. Deep Channel is 22 inches. The fish Mad Ade landed with a net at Little Curl was larger than the one he worked onto shore at Dish Creek, but it was not as large as the one he lifted from the water at Big Little Falls (2). Little Curl is less than 17 inches. 16 inches. Although they both jumped and splashed over the water the same way, the Rainbow Mad Ade caught was bigger than his Cut Throat. (5) So, Rainbow is 22 inches and Cut Throat 19 inches. Summary: 14th, Elk Hair Caddis, Dolly Varden, 16, Little Curl 15th, Stonefly Nymph, Cutthroat, 19, Bottle Well 17th, Mad Ade's Little Mouse, Monkey Trout, 24, Old Cutbank 18th, Mayfly, Brookside Trout, 8, Dish Creek 19th, Yuk Bug, Lake Trout, 27, Big Rock Isle 20th, Parachute Adams, Rainbow, 22, Deep Channel 21st, Humpy, Humpback Trout, 17, Big Little Falls	Mad Ade caught a fish off Big Rock Isle on the 19th (2). The Monkey Trout Mad Ade caught on the 17th (4). Mad Ade caught either the smallest or his second to largest fish on his third fishing day. (1) 17th is 8 or 24.	2.2	3.12	0D	F	5	7	14.8097	null	null	null	14th, Elk Hair Caddis, Dolly Varden, 16, Little Curl 15th, Stonefly Nymph, Cutthroat, 19, Bottle Well 17th, Mad Ade's Little Mouse, Monkey Trout, 24, Old Cutbank 18th, Mayfly, Brookside Trout, 8, Dish Creek 19th, Yuk Bug, Lake Trout, 27, Big Rock Isle 20th, Parachute Adams, Rainbow, 22, Deep Channel 21st, Humpy, Humpback Trout, 17, Big Little Falls
9	Near Orange Bags?	"What's the password?" asked The Entity, with a weasel-like demeanor. Spy IQ was confused, until he realized he had received a strange postcard weeks before. The crafty spy still needed to enter the underground cellar leading to a new set of gadgets to be used on the next mission, but he was halted by The Entity's presence. What the postcard said might help Spy IQ find the password The Entity needs to allow the spy into the secret lair. The postcard says this: A relative of mine was expelled. It was my niece. Wouldn't you agree? It was because she joined a band of bikers. She's doing lots of things wrong. She always shows a lot of toughness. P.S. Isaac Newton: Near orange bags lying east. Gets as strange equally slowly. That P.S. looks like it could be the catalyst to solve for the encrypted password. But, what could it be?	The password is PIGEON. If you look carefully at the P.S., you will notice that the first letter of each word spells IN NOBLE GASES: P.S. [I]saac [N]ewton: [N]ear [O]range [B]ags [L]ying [E]ast. [G]ets [A]s [S]trange [E]qually [S]lowly. Now, look in the first six lines of the postcard. The symbols for noble gases can be found in the last word of each line, with a letter lying in between: a relative of mine was eXpElled. it was my NiEce. wouldn't you AgRee? etc. If you take each letter that is within the symbols of the noble gases, you will spell the word PIGEON: a relative of mine was eX[p]Elled. it was my N[i]Ece. wouldn't you A[g]Ree? it was because she joined a band of biK[e]Rs. she's doing lots of things wR[o]Ng. she always shows a lot of tougH[n]Ess. After saying the password, Spy IQ entered the secret lair and found useful gadgets, including Instant Tile Camouflage.	Look closely at the P.S. A secret message lies within the P.S. that will assist you in searching for the password. Here, I'll change it up a bit: P.S. Isaac Newton: Near Orange Bags Lying East. Gets As Strange Equally Slowly.	2.41	3.11	Pattern	F	x	x	x	x	null	null	PIGEON
10	Lotto Luck	Professor Abacus is purchasing a ticket for the Deca Lotto. The lotto number has ten digits, using the numerals 0 through 9, each numeral used once. The clerk asked what number he wanted to pick. Professor Abacus handed the clerk a piece of paper with nine statements, saying "If you can correctly figure out the number, I will give you half of whatever I win." What is the number? 1) The sum of the first five digits is a prime number. 2) The sum of the last five digits is a triangle number. 3) The sum of the digits in the odd positions is an odd number. 4) The sum of the middle two digits is a square number. 5) The sum of the middle four digits is a cube number. 6) The difference between the 1st and 10th digits is two. 7) The difference between the 2nd and 9th digits is three. 8) The difference between the 3rd and 8th digits is four. 9) The numeral 4 is somewhere in the first five positions. You can form a triangle arrangement by building it in the pattern row 1 = 1, row 2 = 2, row 3 = 3 etc. eg. 10 is a classic triangle number as per ten pin bowling. They are arranged in a triangle 1, 2, 3, 4.	7342105869 7 + 3 + 4 + 2 + 1 = 17 (prime), 0 + 5 + 8 + 6 + 9 = 28 (triangle), 7 + 4 + 1 + 5 + 6 = 23 (odd), 1 + 0 = 1 (square), 2 + 1 + 0 + 5 = 8 (cube), the difference between 7 and 9 is 2, the difference between 3 and 6 is 3, the difference between 4 and 8 is 4, 4 is in the 3rd position.	The sum of all digits must be 45. Combine this with hints 1 and 2 to reduce to a few prime/triangle options	2.23	3.1	Number	F	2	10	6.5598	9	null	null	7342105869
11	Mad Ade's Garden	Mad Ade, Who had suddenly and unexpectedly after years of selfless dedication to Kebabs, decided to grow some vegetable for himself and subsequently planted his garden late in May. He planted five different vegetables: Tomatoes, Peppers, Radishes, Lettuce, and Broccoli. For each he planted a different number of rows from one to five. The hard work involved with each planting was accomplished on a separate day, from May 25th to May 30th (On Sunday May 26th he didn't work in the garden). Each vegetable was planted in a different part of the garden, the north end, the south side, the east side, the west side or the northwest corner. Can you tell which vegetable was planted in each part of the garden, the day planted and the number of rows? 1. Mad Ade turned the soil for the peppers three days after he dug hand-size rocks out of the radish patch. Mad Ade's bright rows of radishes went deeper than the broccoli but were not as deep as the tomatoes. Mad Ade rolled his trusty wheelbarrow into the west end of the garden one day before he planted the broccoli. Mad Ade believes the morning sun is bad for tomatoes and so kept those plants out of the eastern side of his garden. 2. Mad Ade labored hard in the south side of the garden and was mighty proud of the three perfect rows there. On one week's last day, Mad Ade planted the east side of the garden. Mad Ade didn't put the peppers or the tomatoes in the northwest corner. Mad Ade planted an even number of rows in the Northwest corner of his garden. 3. Mad Ade planted three rows before he planted two rows, but planted them after he planted four rows. Mad Ade figured the lettuce wouldn't last long so he planted fewer than three rows. Mad Ade planted the south garden one day before he planted the lettuce. Mad Ade planted more rows of peppers than he did broccoli (which was not planted in the west side of the garden and was not planted the 29th). Which vegetable was planted in how many rows, on which day of May and in which side of Mad Ade's garden?	Please Note that 1.1 refers to clue 1, sentence 1, and thus 2.3 would be clue 2 sentence 3. Explanation: 1.1 Mad Ade turned the soil for the peppers three days after he dug hand-size rocks out of the radish patch. Radishes are 25th or 27th. Peppers are 28th or 30th. 1.3 Mad Ade rolled his trusty wheelbarrow into the west end of the garden one day before he planted the broccoli Broccoli is 28, 29 30 (and West is 27, 28, 29) 3.3 Mad Ade planted the south garden one day before he planted the lettuce. Lettuce 28, 29 30 (and South 27, 28, 29 ) Tomatoes can only be 25th or 27th. 2.2 On one week's last day, Mad Ade planted the east side of the garden. Saturday the 25th is East. 1.4 Mad Ade believes the morning sun is bad for tomatoes and so kept those plants out of eastern side of his garden So East, 25th is not Tomatoes. So Radishes 25th and Tomatoes 27th. And 3 days later 28th = peppers. 3.4 Mad Ade planted more rows of peppers than he did broccoli (which was not planted in the west side of the garden and was not planted the 29th). So Broccoli 30th and Lettuce 29th. 1.3 Mad Ade rolled his trusty wheelbarrow into the west end of the garden one day before he planted the broccoli. West is 29th. 3.2 Mad Ade figured the lettuce wouldn't last long so he planted fewer than three rows. So Lettuce is one or two rows. 2.4 Mad Ade planted an even number of rows in the Northwest corner of his garden. Northwest is 2 or 4 rows. 1.2 Mad Ade's bright rows of radishes went deeper than the broccoli but were not as deep as the tomatoes. Radishes are not one or five. Broccoli is not five or four. Tomatoes is not one or two. 2.3 Mad Ade didn't put the peppers nor the tomatoes in the northwest corner. Northwest is broccoli. Lettuce has one row. 2.1 Mad Ade labored hard in the south side of the garden and was mighty proud of the three perfect rows there. So South is three rows. Radishes are four. 3.3 Mad Ade planted the south garden one day before he planted the lettuce. So planted 3 in south on 28. Five rows of tomatoes were planted in the North Garden. Summary: Tomatoes, Five, 27th, North Peppers, Three, 28th, South Radishes, Four, 25th, East Lettuce, one, 29th, West Broccoli, two, 30th, Northwest	Start by deducing which vegetables pair with which dates	2.27	3.09	0D	F	4	5	6.2375	12	null	null	Tomatoes, Five, 27th, North Peppers, Three, 28th, South Radishes, Four, 25th, East Lettuce, one, 29th, West Broccoli, two, 30th, Northwest
12	Bingo Card 4	You are given a stack of bingo cards. Your task is to find a specific card. Given the following clues, what is the number arrangement of that card? Columns, left to right, are: B (contains numbers 1 through 15), I (contains numbers 16 through 30), N (contains numbers 31 through 45), G (contains numbers 46 through 60), O (contains numbers 61 through 75). Rows, top to bottom, are: 1, 2, 3, 4, 5. An example of coordinate nomenclature: B1 identifies column B row 1. N3 is a free space (contains no number). No number appears more than once. 1) Each numeral (0 through 9) appears one time in Row 1. 2) The sum of the numbers in Row 4 is a square number. 3) There is only one two-digit prime number in each row. 4) The range of the numbers in Column N is 8. 5) Each number in Column G has a tens digit that is less than the units digit. 6) Each number in Column O is odd. 7) In only one column are the numbers in descending order from top to bottom. 8) Each column has only one numeral that appears exactly two times. 9) The smallest number in each column is located in Row 5. 10) The sums of each column share a single common prime factor. 11) The numeral 5 only appears one time on the card. 12) The sum of the numbers in each diagonal is an odd number. 13) The product of B3 and O3 has a units digit of 2. 14) The product of I3 and G3 has a units digit of 4.	10 24 39 58 67 9 28 40 49 71 8 22 -- 47 69 3 30 42 48 73 1 20 34 46 61 1) Per clue 5, eliminate the appropriate numbers in Column G. Of the remaining numbers, at least one with a tens digit of 5 will have to be used. Per clues 1 and 11, only one number can have the numeral 5, so that number must be at G1. Eliminate all numbers that contain a 5 from all other locations. 2) Per clue 6, eliminate all even numbers from Column O. 3) Per clue 1, eliminate any number from Row 1 with only one digit or duplicate digits. By analyzing combinations of numbers, the following can be determined: B1 contains a 1, delete 30, I1 contains a 2, delete 23, delete 63 and 73, O1 contains a 6. In conjunction with clue 3, delete 29 and 59. 4) Per clue 10, analyze the various possible sums of Columns G and O. The only common prime factor is 31. Each column must sum to a multiple of 31 (based on available numbers: B to 31, I to 124, N to 155, G to 248, and O to 341). G1 must be 58. All two-digit prime numbers (clue 3) must be in Columns G and O. O1 must be 67. Per clue 1, N1 must be 39. Per clue 9, G5 must be 46 and O5 must be 61. 5) For Column N, there is only set of numbers that sums to 155, and satisfies clues 4, 8, and 9 (34, 39, 40, 42). N5 must be 34. 6) For Column I, there are two sets of numbers that sum to 124, and satisfy clues 8 and 9 (16, 24, 26, 28, 30 and 20, 22, 24, 28, 30). To satisfy clue 1, I1 must be 24. B1 must be 10. To satisfy clue 12, G4 must be 48 and B5 must be odd. 7) The column that satisfies clue 7 is Column B. To satisfy clue 8, B2 must be 9 and B5 must be 1. 8) To satisfy clue 2, the only square number that can be achieved is 196. B4 must be 3, I4 must be 30, N4 must be 42, and O4 must be 73. 9) B3 must be 8. N2 must be 40. 10) To satisfy clue 13, O3 must be 69. This leaves O2 being 71. To satisfy clue 3, G3 must be 47. This leaves G2 being 49. 11) To satisfy clue 14, I3 must be 22. Finally, to achieve a sum of 124 (multiple of 31), I2 must be 28 and I5 must be 20.	Start with clue 5!	1.88	3.08	2D	F	2	25	27.7837	14	null	null	10 24 39 58 67 9 28 40 49 71 8 22 -- 47 69 3 30 42 48 73 1 20 34 46 61
13	Mystery Number 8	There is a ten digit mystery number (no leading 0), represented by ABCDEFGHIJ, where each numeral, 0 through 9, is used once. Given the following clues, what is the number? 1) If A > B, then C = 5 or 7, else C = 0 or 1. 2) If B > C, then D = 1 or 2, else D = 4 or 9. 3) If C > D, then E = 6 or 9, else E = 3 or 5. 4) If D > E, then F = 2 or 4, else F = 1 or 6. 5) If E > F, then G = 5 or 6, else G = 0 or 7. 6) If F > G, then H = 1 or 4, else H = 8 or 9. 7) If G > H, then I = 0 or 8, else I = 6 or 7. 8) If H > I, then J = 3 or 8, else J = 2 or 5. 9) If I > J, then A = 3 or 7, else A = 4 or 8. 10) If J > A, then B = 0 or 9, else B = 2 or 3.	8274965103 A = 8, B = 2, C = 7, D = 4, E = 9, F = 6, G = 5, H = 1, I = 0, J = 3 1) A = 8 (I < J) 2) B = 2 (J < A) 3) C = 7 (A > B) 4) D = 4 (B < C) 5) E = 9 (C > D) 6) F = 6 (D < E) 7) G = 5 (E > F) 8) H = 1 (F > G) 9) I = 0 (G > H) 10) J = 3 (H > I) Brute force methods can be used to arrive at a solution. However, process of elimination does work. For example, assign 8 to H. I can not exceed H, so J would have to be 3 (8 already assigned to H). G can not exceed H, so I would have to be either 6 or 7. I would be greater than J, so A would have to be 7 (3 already assigned to J), meaning I would have to be 6. J is less than A, so B would be 2 (3 already assigned to J). A is greater than B, so C would be 5 (7 already assigned to A). The only remaining numeral for G is 0, which means F would have to be greater than G, meaning H would have to be either 1 or 4. H has already been assigned 8, rendering that assignment impossible. Continue eliminating possibilities in the order shown below. A) H can not be 8. C can not be 1. C can not be 0. B can not be 9. D can not be 1. D can not be 2. F can not be 1. B) H must be 1. H can not be 4. H can not be 9. C) G can not be 0. I can not be 6. I can not be 7. B can not be 0. D) I must be 0. I can not be 8. E) J can not be 2. J can not be 5. J can not be 8. F) J must be 3. A can not be 3. B can not be 3. E can not be 3. G) B must be 2. F can not be 2. H) A must be 8. A can not be 4. A can not be 7. I) D can not be 9. J) E must be 9. E can not be 5. E can not be 6. K) D must be 4. F can not be 4. L) F must be 6. G can not be 6. M) G must be 5. C can not be 5. G can not be 5. N) C must be 7.	For example, assign 8 to H. I can not exceed H, so J would have to be 3 (8 already assigned to H).	2.11	3.07	Compound	F	2	10	6.51401	10	Number	null	8274965103
14	Mystery Number 6	There is a ten-digit mystery number (no leading 0), represented by ABCDEFGHIJ, where each numeral, 0 through 9, is used once. Given the following clues, what is the number? 1) Digit A is either a square number or a triangle number, but not both. 2) Digit B is either an even number or a cube number, but not both. 3) Digit C is either a cube number or a triangle number, but not both. 4) Digit D is either an odd number or a square number, but not both. 5) Digit E is either an odd number or a cube number, but not both. 6) Digit F is either an odd number or a triangle number, but not both. 7) Digit G is either an odd number or a prime number, but not both. 8) Digit H is either an even number or a square number, but not both. 9) Digit I is either a square number or a cube number, but not both. 10) Digit J is either a prime number or a triangle number, but not both. 11) A < B, C < D, E < F, G < H, I < J 12) A + B + C + D + E < F + G + H + I + J	3605891247 A = 3, B = 6, C = 0, D = 5, E = 8, F = 9, G = 1, H = 2, I = 4, J = 7 1) 3 is a triangle number, but not a square number. 2) 6 is an even number, but not a cube number. 3) 0 is a cube number, but not a triangle number. 4) 5 is an odd number, but not a square number. 5) 8 is a cube number, but not an odd number. 6) 9 is an odd number, but not a triangle number. 7) 1 is an odd number, but not a prime number. 8) 2 is an even number, but not a square number. 9) 4 is a square number, but not a cube number. 10) 7 is a prime number, but not a triangle number. 11) 3 < 6, 0 < 5, 8 < 9, 1 < 2, 4 < 7 12) 3 + 6 + 0 + 5 + 8 = 22, 9 + 1 + 2 + 4 + 7 = 23, 22 < 23 A) First, determine what two subsets of numbers qualify for each digit. However, each digit can only be in one of the subsets, not both. B) Digit A can not be 0 (a leading zero is not allowed). C) Next, eliminate those numbers that do not satisfy Condition 11. Digit I can only be 4. Digit A can only be 3. Digit B can only be 6. Digit C can only be 0. D) Digit D and Digit J must be some combination of 5 and 7. Digit E can only be 8. Digit F can only be 9. Digit G can only be 1. Digit H can only be 2. E) To satisfy Condition 12, Digit D is 5 and Digit J is 7.	A) First, determine what two subsets of numbers qualify for each digit. However, each digit can only be in one of the subsets, not both.	1.96	3.07	Compound	F	2	10	6.51401	12	Number	null	3605891247
15	Einstein's Riddle	Einstein's Riddle: Einstein wrote the following riddle. He said that 98% of the world could not solve it. But several NIEHS scientists were able to solve it, and they said it's not all that hard if you pay attention and are very patient. Give it a try: There are 5 houses in 5 different colors in a row. In each house lives a person with a different nationality. The 5 owners drink a certain type of beverage, smoke a certain brand of cigar, and keep a certain pet. No owners have the same pet, smoke the same brand of cigar, or drink the same beverage. Other facts: 1. The Brit lives in the red house. 2. The Swede keeps dogs as pets. 3. The Dane drinks tea. 4. The green house is on the immediate left of the white house. 5. The green house's owner drinks coffee. 6. The owner who smokes Pall Mall rears birds. 7. The owner of the yellow house smokes Dunhill. 8. The owner living in the center house drinks milk. 9. The Norwegian lives in the first house. 10. The owner who smokes Blends lives next to the one who keeps cats. 11. The owner who keeps the horse lives next to the one who smokes Dunhill. 12. The owner who smokes Bluemasters drinks beer. 13. The German smokes Prince. 14. The Norwegian lives next to the blue house. 15. The owner who smokes Blends lives next to the one who drinks water. The question is: WHO OWNS THE FISH?	The German sits in his Green House, smoking his Prince cigars, drinking coffee, and watching his FISH. The rest go like this- 1st House: Yellow, Norwegian, Water, Cats, Dunhill 2nd House: Blue, Dane, Tea, Horse, Blends 3rd House: Red, Brit, Milk, Birds, Pall Malls 4th House: Green, German, Coffee, FISH, Prince 5th House: White, Swede, Beer, Dogs, Bluemasters	Just take your time. This one should take you some time and is probably one of the harder riddles you see.	3.07	3.04	1D	H	6	5	10.3959	15	null	null	The German sits in his Green House, smoking his Prince cigars, drinking coffee, and watching his FISH
16	Battleship Tournament	The first round of the Children's Battleship Tournament has just been concluded. Our ten contenders (including Roger and Lila) have just concluded their first five exciting matches. Each match consisted of two players facing off against each other trying to guess the locations of the other player's ships. (The Carrier covers 5 squares, the Battleship covers 4 squares, the Destroyer and Submarine each cover 3 squares, and the Patrol Boat covers 2 squares.) In the end of each match, only one of the winner's ships remained - and it was a different one in each match! From the information given, can you determine the full name of the winner and loser of each match, as well as the remaining ship of the winner? 1. Alexis Chartel, although managing to sink her opponent's Carrier and Patrol Boat, still lost; her opponent was not surnamed Roon. 2. The surviving ship of the kid whose last name is Azzuro (who is not Jason) is shorter than the surviving ship of the player that beat the kid surnamed Yeller. 3. The kid who defeated Charlie won because of his or her surviving Submarine. 4. Fred (who is not surnamed Blanc) lost to the kid who's last name is Black (who is not Bart). 5. One of the matches was between the players surnamed Lavender and Tanger. 6. Three - and only three - of the matches were between one boy and one girl. 7. The five games were the one Stacie won (but the loser was not surnamed Chartel), the one Patty lost, the one won by the boy who's last name is Brown, the one lost by the kid who's last name is Blanc, and the one where the only surviving ship was a Patrol Boat (who's last name is not Black). 8. Bart managed to have his Carrier survive the entire game, thus winning his game. 9. The kids surnamed Peach and Lavender had the same result in their matches. 10. Georgia Roon won her match, but not against Patty or Charlie.	From clue 1, Alexis' last name is Chartel, and she lost. From clue 3. Charlie lost the game where the surviving ship was the Submarine. From clue 4, Fred lost to Black. From clue 8, Bart won the game where the surviving ship was the Carrier; from clue 4, he is not Black, and from clue 1, he did not defeat Alexis, so he was in a fourth game. From clue 10, Georgia's last name is Roon, and she won, but not against Charlie, and from clue 1, not against Alexis, so she was in a fifth match. So five matches are: _____ _____ beat Alexis Chartel by a _____. Bart _____ beat _____ _____ by a Carrier. _____ _____ beat Charlie _____ by a Submarine. _____ Black beat Fred _____ by a _____. Georgia Roon beat _____ _____ by a _____. Patty did not lose to Georgia (clue 10); she lost to Bart. Alexis Charlet was not defeated by Stacie (clue 7), nor was the surviving ship the Patrol Boat (clue 1); she was defeated by Brown (only one left in clue 7). Fred is not Blanc (clue 4), nor was the surviving ship the Patrol Boat (clue 7); he was defeated by Stacie (only one left in clue 7). Charlie is Blanc (only one left in clue 7), so Georgia Roon won with her Patrol Boat (only one left in clue 7). Meaning: Stacie Black beat Fred _____ by a _____ Bart _____ beat Patty _____ by a Carrier. _____ Brown beat Alexis Chartel by a _____. _____ _____ beat Charlie Blanc by a Submarine. Georgia Roon beat _____ _____ by a Patrol Boat. The only match in which Lavender and Tanger could face each other is the one where Bart beat Patty - but we don't know which last name goes with which kid. The only remaining winner that Azzuro could be is the one that beat Charlie. Yeller cannot have lost to Georgia (Patrol Boat is shorter than Submarine - clue 2); he is Fred, and his opponent won with a Battleship (only remaining ship longer than a Submarine - clue 2), so Brown beat Alexis with a Destroyer (only ship left). Meaning: Stacie Black beat Fred Yeller by a Battleship. Bart _____ beat Patty _____ by a Carrier. _____ Brown beat Alexis Chartrel by a Destroyer. _____ Azzuro beat Charlie Blanc by a Submarine. Georgia Roon beat _____ _____ by a Patrol Boat. The only place for the last name Peach is as the kid who lost to Georgia. Since Peach lost, Lavender must have lost (clue 9) and Tanger must have won. Two of the matches are known to be between a boy and a girl. The other three must be one between a boy and a girl (clue 6), one between two boys (two of the unplaced kids are boys, and only one of them could be in the third boy/girl match), and one between two girls (two of the placed kids with unplaced opponents are girls, and only one of them could be in the third boy/girl match). Charlie must be facing a boy who's last name is Azzuro, but it's not Jason (clue 2); it's Roger. Brown cannot be Lila (clue 7); he's Jason, so Lila is Peach (only possibility). In summary: Bart Tanger beat Patty Lavender by a Carrier. Stacie Black beat Fred Yeller by a Battleship. Jason Brown beat Alexis Chartel by a Destroyer. Roger Azzuro beat Charlie Blanc by a Submarine. Georgia Roon beat Lila Peach by a Patrol Boat.	In case you need all the kid's names: The boys are Bart, Charlie, Fred, Jason, and Roger. The girls are Alexis, Georgia, Lila, Patty, and Stacie. The last names are Azzuro, Black, Blanc, Brown, Chartrel, Lavender, Peach, Roon, Tanger, and Yeller.	2.57	3.04	0D	F	3	5	6.55976	10	null	null	Bart Tanger beat Patty Lavender by a Carrier. Stacie Black beat Fred Yeller by a Battleship. Jason Brown beat Alexis Chartel by a Destroyer. Roger Azzuro beat Charlie Blanc by a Submarine. Georgia Roon beat Lila Peach by a Patrol Boat.
17	16 Coins	Johnny was given 16 coins by his older, somewhat meaner brother, Mark. He told him that he could keep them all if he could place all 16 on the table in such a way that they formed 15 rows with 4 coins in each row. After 10 minutes, Johnny walked away with the coins and Mark, after complaining futilely to his mother, left with nothing. How did Johnny place the coins?	If you draw a 5-pointed star with all sides of equal length, you will create a pentagon in the middle with all 5 sides of equal length. Then draw another 5 pointed star, upside-down, using the 5 points of the interior pentagon as the points of the inner star, This will give you another 5-sided pentagon in the interior of the second, smaller star. Now, take your 16 coins and place 5 on the outside points of the outside star. Then place 5 more on the points of each of the two pentagons you have created. Finally, place the last coin in the dead center of this drawing. The lines are as follows: 5 lines for the actual drawing of the outside star 5 lines for the actual drawing of the inside star 5 lines that start from any outside point of the outside star and go to the opposite point of the inside star, passing through 1 point of the inner pentagon, the dead center coin on the way. Total lines: 15	Stars and pentagons	2.8	3.03	Algorithm	A	x	x	x	x	Y	null	"If you draw a 5-pointed star with all sides of equal length, you will create a pentagon in the middle with all 5 sides of equal length. Then draw another 5 pointed star, upside-down, using the 5 points of the interior pentagon as the points of the inner star, This will give you another 5-sided pentagon in the interior of the second, smaller star. Now, take your 16 coins and place 5 on the outside points of the outside star. Then place 5 more on the points of each of the two pentagons you have created. Finally, place the last coin in the dead center of this drawing. The lines are as follows: 5 lines for the actual drawing of the outside star 5 lines for the actual drawing of the inside star 5 lines that start from any outside point of the outside star and go to the opposite point of the inside star, passing through 1 point of the inner pentagon, the dead center coin on the way. Total lines: 15"
18	Bingo Card	You are given a stack of bingo cards. Your task is to find a specific card. Given the following clues, what is the number arrangement of that card? Columns, left to right, are: B (contains numbers 1 through 15), I (contains numbers 16 through 30), N (contains numbers 31 through 45), G (contains numbers 46 through 60), O (contains numbers 61 through 75). Rows, top to bottom, are: 1, 2, 3, 4, 5. An example of coordinate nomenclature: B1 identifies column B row 1. N3 is a free space (contains no number). No number appears more than once. 1) All numbers in row 2 are divisible by 2; all numbers in row 3 are divisible by 3; all numbers in row 4 are divisible by 4; all numbers in row 5 are divisible by 5. 2) Row 2: the units digits are the same. 3) Row 4: the units digits are all different. 4) Row 5: the sum of the numbers is divisible by 7. 5) Column B: contains five consecutive numbers (in any order). 6) Column I: three of the numbers are odd. 7) Column G: three numbers are divisible by 3; three numbers are divisible by 4; one number is divisible by 12. 8) Column O: the sum of the five numbers is an odd number. 9) The product of I3 and G3 is between 1300 and 1400. 10) The sum of B1 and O1 is 82. 11) The difference between N1 and N5 is 1. 12) N2 is midway between B4 and O4. 13) N4 is midway between I1 and G1.	7 23 44 57 75 6 26 36 56 66 9 27 -- 51 72 8 16 40 52 64 10 25 45 60 70 1) Per clue 1, eliminate the appropriate numbers in the various rows. 2) Per clue 6, since rows 2 and 4 must contain even numbers, the other three rows in column I must contain odd numbers. I5 must be 25. 3) Per clue 7, G5 must be 60. 4) Per clue 9, I3 must be 27 and G3 must be 51. 5) Per clue 13, since I1 is odd, then G1 must be odd. G1 must be 57. I1 must be 23. N4 must be 40. 6) Per clue 10, B1 can not be less than 7 and O1 can not be less than 67. 7) Per clue 2, based on G2, no number in row 2 can end in 0 or 4 or 8. 8) Per clue 5, eliminate impossible combinations in column B. 9) Per clue 12, eliminate numbers that can not work. N2 must be 36. O4 must be either 64 or 68. 10) Per clue 2, the units digits is 6. B2 must be 6. G2 must be 56. O2 must be 66. This leaves G4 as 52. 11) Per clue 5, eliminate impossible combinations in column B. B1 must be 7. 12) Per clue 10, O1 must be 75. 13) Per clue 3, I4 must be 16. This leaves I2 as 26. 14) Per clue 4, in order for the sum of row 5 to be divisible by 7, the sum must be either 175 or 210. Since I5 must be 25 and G5 must be 60, then the sum must be 210. B5 must be 10. N5 must be 45. O5 must be 70. 15) Per clue 5, B3 must be 9 and B4 must be 8. 16) Per clue 3, O4 must be 64. 17) Per clue 8, O3 must be 72. 18) Per clue 11, N1 must be 44.	Start with clue 1 to eliminate numbers in various rows	2.41	3.03	2D	F	2	25	27.7837	13	null	null	7 23 44 57 75 6 26 36 56 66 9 27 -- 51 72 8 16 40 52 64 10 25 45 60 70
19	Menagerie	Zachary has a private zoo. He has five groups of animals in his zoo: snakes, birds, mammals, insects, and spiders. Assume that, typically: animals have 1 head, snakes have 0 legs, birds have 2 legs, mammals have 4 legs, insects have 6 legs, and spiders have 8 legs. Zachary has some unusual animals in his zoo. He has: a snake with 3 heads, a bird with 2 heads, a mammal with 3 legs, an insect with 4 legs, and a spider with 7 legs. From the following information, determine how many of each group of animals that Zachary has in his menagerie. 1) There are a total of 100 heads and 376 legs. 2) Each group has a different quantity of animals. 3) The most populous group has 10 more members than the least populous group. 4) There are twice as many insect legs as there are bird legs. 5) There are as many snake heads as there are spider heads.	A) Since there are 3 extra heads (2 snake and 1 bird), there are only 97 animals (clue 1). Find a set of five different numbers whose sum is 97 (clue 2) and whose size difference between the least populous and most populous group is 10 (clue 3). There are 17 sets that meet these requirements. 13, 18, 21, 22, 23 13, 19, 20, 22, 23 14, 15, 21, 23, 24 14, 16, 20, 23, 24 14, 16, 21, 22, 24 14, 17, 19, 23, 24 14, 17, 20, 22, 24 14, 18, 19, 22, 24 14, 18, 20, 21, 24 15, 16, 17, 24, 25 15, 16, 18, 23, 25 15, 16, 19, 22, 25 15, 16, 20, 21, 25 15, 17, 18, 22, 25 15, 17, 19, 21, 25 15, 18, 19, 20, 25 16, 17, 18, 20, 26 B) There are twice as many insect legs as there are bird legs (clue 4). To find the possible bird and insect group sizes, multiply the quantity of insects by 6 (legs per insect). Subtract 2 (an insect is missing 2 legs). Divide by 2 (twice as many insect legs as bird legs). Divide by 2 (legs per bird) to get the quantity of birds. The formula is: B = ((I * 6) - 2) / 4. There are three combinations that work: 13 and 19, 15 and 22, 17 and 25. ((13 insects * 6 legs/insect) - 2 missing legs) / 4 = 19 birds ((15 insects * 6 legs/insect) - 2 missing legs) / 4 = 22 birds ((17 insects * 6 legs/insect) - 2 missing legs) / 4 = 25 birds Of the 17 sets (from step A), only 5 contain these sizes. 13, 19, 20, 22, 23 (13 insects & 19 birds) 15, 16, 17, 24, 25 (17 insects & 25 birds) 15, 16, 19, 22, 25 (15 insects & 22 birds) 15, 17, 18, 22, 25 (15 insects & 22 birds or 17 insects & 25 birds) 15, 17, 19, 21, 25 (17 insects & 25 birds) C) There are as many snake heads as spider heads (clue 5). Since there is a snake with two extra heads, there are actually 2 fewer snakes compared to spiders. Only 2 combinations (from step B) yield the required head count. 13 insects, 19 birds, 20 snakes, 22 spiders, 23 mammals 15 mammals, 17 insects, 19 snakes, 21 spiders, 25 birds D) The only group combination (from step C) that produces 376 legs (clue 1) is: 15, 17, 19, 21, 25. The other combination yields 380 legs. (15 mammals * 4 legs/mammal) - 1 missing leg = 59 legs (17 insects * 6 legs/insect) - 2 missing legs = 100 legs 19 snakes * 0 legs/snake = 0 legs (21 spiders * 8 legs/spider) - 1 missing leg = 167 legs 25 birds * 2 legs/birds = 50 legs Thus, there are: 19 snakes (21 heads and 0 legs), 25 birds (26 heads and 50 legs), 15 mammals (15 heads and 59 legs), 17 insects (17 heads and 100 legs), and 21 spiders (21 heads and 167 legs). This produces 97 animals with 100 heads and 376 legs.	Since there are 3 extra heads (2 snake and 1 bird), there are only 97 animals (clue 1). Find a set of five different numbers whose sum is 97 (clue 2) and whose size difference between the least populous and most populous group is 10 (clue 3).	2.34	3.03	Math	F	x	x	x	x	null	null	19 snakes (21 heads and 0 legs), 25 birds (26 heads and 50 legs), 15 mammals (15 heads and 59 legs), 17 insects (17 heads and 100 legs), and 21 spiders (21 heads and 167 legs)
20	Murder on the ABC Express	The ABC Express pulled out of the station late one night and began its winding journey up the coast to its destination under heavy darkness. Owing to the late hour, there were only a handful of passengers aboard the small train. At the stroke of midnight, the lights illuminating the interior of the two cars were suddenly extinguished. When they flicked back to life a few moments later, the passengers were alarmed to see one of their number lying on the ground motionless. The conductor phoned the local police department, and though it was very late, the dispatcher assured the worried conductor that they were sending their very best detective. A bit of an eccentric, Detective Y had an usual methodology when it came to solving crimes. Knowing witnesses to be often be mistaken and contradictory, Y made a habit of asking his witnesses to state to him only one fact they remembered clearly and with absolute certainty from the moment the crime took place. Y wasted no time upon arriving and, after taking a quick overview of the scene, asked each of the ten remaining passengers in turn to state one absolute fact from the moment right before lights went out in the two train cars. His interview notes are as follows: Ms. S: I was dining with Mr. J. Mr. G: There were the same number of men and women in my car. Mr. J: Mr. K was not in the dining car. Ms. L: Mr. Q had just entered my car. Mr. F: Ms. W and Ms. P were talking to one another in hushed tones. Mr. R: Mr. G was not in the passenger car. Mr. Q: There were fewer women in my car than the other. Ms. P: Ms. L was not in the same car as me. Mr. K: Ms. P was in the passenger car. Ms. W: Mr. F was avoiding Mr. R and hiding behind a newspaper in the opposite car. The bewildered conductor watched as Detective Y completed his interviews, scribbled a few more lines in his notes, and turned to announce he had solved the case. "But surely you can't have figured out the identity of a murderer simply from a list of seating arrangements?" the conductor protested. "You haven't even been told in which car the victim was seated!" "To the contrary, my good man," the detective answered placidly. "It is the curse of a criminal that he must answer any question regarding the crime he has committed with a lie. The innocent tell only truths, but the lone murderer has been betrayed by his testimony." Who did Detective Y arrest?	Y began by assuming everyone was telling the truth about each other's location and came up with the following arrangement: S J L Q G R (4 men, 2 women) in the dining car and K P W F (2 men, 2 women) in the passenger car. (R and F are interchangeable in this scenario, but as both are men, the precise position of each is irrelevant to this point.) This contradicted both G's statement that there were an equal number of men and women in his (the dining) car and Mr. Q's claim that fewer women were in one car than the other. Thus, the detective concluded both G and Q were telling the truth and someone was lying about the occupancy. Y reasoned that only one possible configuration could make both men's testimonies true: G, 2 other men, and 3 women in one car and Q, 2 other men, and 1 woman in the other. Because G and Q had to have been in opposite cars, Y worked back up his witness list to find the lie that had placed Q in the wrong car. He first examined L's statement that she and Q shared the same car. If this alone was the lie, it would leave S J L G R (3 men, 2 women) in the dining car and put K P Q W F (3 men, 2 women) in the passenger car, meaning G and Q's statements still would be inaccurate. Ms. L must be telling the truth then, and Y instead turned to P's claim, which had placed L (and Q by extension) in the other car. If P was lying, it would mean only S J G R (3 men, 1 woman) were in the dining car and K P L Q W F (3 men, 3 women) were in the passenger car. Again, neither G or Q's statements are met. Detective Y, now certain Mr. G, Mr. Q, Ms. L, and Ms. P were all telling the truth, backtracked to Mr. K next, who had established P's position. Assuming K a liar, Y was able to place S J P G W R (3 men, 3 women) in the dining car and K L Q F (3 men, 1 woman) in the passenger car. A prudent man, Y double checked his work by running each remaining statement against his reasoning and stiffened his resolve upon finding K to be the only possible person whose lone lie could make every other witness statement truthful. Mr. K was arrested and led away to the relief (albeit, slight puzzlement) of the conductor and his passengers.	Like any good Detective, Y always assumes everyone he interviews is telling the truth until proven otherwise. He also knows the simplest explanation is always the best. He compares the witness statements until he discovers the scenario that is accurately described by nine truthful witnesses and arrests the liar.	3	3.02	Liars	H	2	10	3.0103	10	null	null	Mr. K
21	Seven Sportsmen	Seven sportsmen are standing in a row. Each sportsman has a different 1-digit number. The product of the first three, the product of the middle three, and the product of the last three are all equal. What's the middle sportsman's number?	Let their numbers be a through g, we have abc=cde=efg. 5 or 7 cannot occur, because they are prime and no other 1-digit number contains them. Therefore, the numbers are 1, 2, 3, 4, 6, 8, 9. Since abc=efg, abcdefg/d is a perfect square. 1234689=2^73^4, and d can be only 2 or 8. If d=2, the numbers 1, 3, 4, 6, 8, 9 can be made into 189=346=72, and we can have c=9, e=4: 924=72. If d=8, the numbers 1, 2, 3, 4, 6, 9 can be made into 149=23*6=36, but 36 is not divisible by 8. Therefore, the middle sportsman's number is 2.	Figure out what the numbers are, and then eliminate the impossibilities.	2.57	3.02	Number	H	2	7	5.78161	1	null	null	2
22	Survival of the People	The Situation: There is an island with 10 inhabitants. One day a monster comes and says that he intends to eat every one of them but will give them a chance to survive in the following way: In the morning, the monster will line up all the people - single file so that the last person sees the remaining 9, the next person sees the remaining 8, and so on until the first person that obviously sees no one in front of himself. The monster will then place black or white hats on their heads randomly (they can be all white, all black or any combination thereof). The monster will offer each person starting with the last one (who sees everyone else's hats) to guess the color of his/her own hat. The answer can only be one word: "white" or "black". The monster will eat him on the spot if he guessed wrong, and will leave him alive if he guessed right. All the remaining people will hear both the guess and the outcome of the guess. The monster will then go on to the next to last person (who only sees 8 people), and so on until the end. The monster gives them the whole night to think. The Task: Devise the optimal strategy that these poor natives could use to maximize their survival rate. Assumptions: 1) All the 10 people can easily understand your strategy, and will execute it with perfect precision. 2) If the monster suspects that any of the people are giving away information to any of the remaining team members by intonation of words when answering, or any other signs, or by touch, he will eat everyone. 3) The only allowed response is a short, unemotional "white" or "black". 4) Having said that, I will add that you can put any value you like into each of these words. For example, "white" can mean "my mother did my laundry" and "black" can mean the guy in front of me is wearing a black hat.	Here it is: The first guy to guess (guy #10) will be the only one to assume the following value for the words "white" and "black": The answer "black" will mean that there are an odd number of black hats that he sees. The answer "white" will mean that there are an odd number of white hats that he sees. This way one by one all the other 9 people will know the color of their hats. Let us say that guy #10 (first to speak, and sees the hats of the remaining 9) says "white". That should mean to everybody else that he sees an odd number of white hats. At this time guy #9 will either be wearing a white or a black hat. If he is wearing a white hat he will only see an even number of white hats, and since guy #10 said that there is and odd number of white hats, guy #9 will know that he is wearing white and will say it. But if guy #9 is wearing a black hat, he will see an odd number of white hats (just like #10 did), and thus will know that he is wearing a black hat and will say it. No matter what #9 answers, guy #8 (who heard guy #10 and guy #9) can now easily incorporate the color of hat on guy #9 into the original answer of guy #10. This will allow #8 to know if he should see an odd or even number of white hats in front of him to determine his own hat color. The same thing repeats with #7-1. And they all get it right except of course #10, though he may get lucky.	1) First hint is an example. Here is a simple strategy that will guarantee safety to 50%. Guy #10 (when he guesses) says the color of the hat on guy #9. Thus #10 may die or may luck out, but #9 will save himself since he will know his hat color. Thus #8 helps #7, #6 helps number #5, and so on. You thus save numbers 9, 7, 5, 3, and 1, or half the people. But you can do a lot better than that. 2) The best strategy will save a minimum of 90% of the people.	3.05	3.01	Algorithm	A	x	x	x	x	Communication	null	Here it is: The first guy to guess (guy #10) will be the only one to assume the following value for the words "white" and "black": The answer "black" will mean that there are an odd number of black hats that he sees. The answer "white" will mean that there are an odd number of white hats that he sees. This way one by one all the other 9 people will know the color of their hats. Let us say that guy #10 (first to speak, and sees the hats of the remaining 9) says "white". That should mean to everybody else that he sees an odd number of white hats. At this time guy #9 will either be wearing a white or a black hat. If he is wearing a white hat he will only see an even number of white hats, and since guy #10 said that there is and odd number of white hats, guy #9 will know that he is wearing white and will say it. But if guy #9 is wearing a black hat, he will see an odd number of white hats (just like #10 did), and thus will know that he is wearing a black hat and will say it. No matter what #9 answers, guy #8 (who heard guy #10 and guy #9) can now easily incorporate the color of hat on guy #9 into the original answer of guy #10. This will allow #8 to know if he should see an odd or even number of white hats in front of him to determine his own hat color. The same thing repeats with #7-1. And they all get it right except of course #10, though he may get lucky.
23	I Read You 5x5	"Congratulations, Great-Aunt Nora!" The voice of Victor Summ, her eldest nephew, was tired, but exultant. Her older sister was the first grandparent among the five Shekrie siblings. "Let me put you on speaker-phone, Vic. Corman is here." Nora had little doubt that her romance with a math teacher was the reason Victor, a research statistician, called personally, instead of letting his mother handle the news. Nora beamed at Corman as she hit the button. "You're on, 'Daddy'. Mother and children are doing fine?" "Cogita's doing great, although we had a bit of a shuffle in the maternity ward. Hi, Professor diNoni -- you'll love this one." "Hi, Victor. I've heard more about you than ... no, you've known your aunt longer. You probably know how much she's talked about you." "It runs in the family," he smiled across two time zones. "Doc Matter, our OB, said it was the strangest coincidence she's seen in a decade. The kids were born 10, 20, 30, minutes apart, up to an interval of an hour-fifty ..." Vic's voice trailed off. "Except for one interval?" Corman filled in. "Right. She said it was really weird, watching the time. She said Adele was born at six sharp, Brand at 6:10, and they just kept hitting 10-minute multiples, until Elana came out at 7:50." Nora yelped. "You had eleven," then her left brain caught up, "no, just the quintuplets. Sorry." "De nada, Aunt Nora. But that's where the problems started: they had the birth order mixed up. Someone had assumed we'd named them in order, with Brand, Caleb, and Derec in between. I pointed out that they'd managed to get all five wrong, and then Cogita wanted me." "So they got it sorted out?" "Not quite. The OB saw to the post-delivery stuff while we beamed at each other. Then a nurse came in and said they figured it out: we'd named them in alphabetical order, but by the last letter of their names. They had all five wrong again! Heck, even if we'd done it in reverse alphabetical order, either way, they would have had all five wrong!" "So what did they do?" "Doc Matter said she may be getting gray, but she wasn't going to sign the certificates until they were all correct. She dictated the birth times and told them to match them with the weight and length stats to sort things out -- and if they couldn't, they shouldn't bother reporting for work after tonight." He took a cleansing breath. "On a happier note, we'd like the blood aunts and uncles to serve as godparents, since there are five of you. Would you stand for Caleb, Aunt Nora, since the two of you have the same birth position in the family?" "I'd love to. And if anyone in this family declines, I'll have Corman make them figure out the birth order. Do you have it yet, dear?" Vic broke in, "He doesn't have enough information yet, and I can hear you smirking at him." Corman held up a hand to keep her quiet. "Since I don't know much about Nora's birth order, I'll have to make this a bigger question. How far apart were Brand and Elena born?" "Fifty minutes, on their cute little noses." "Got it." Corman recited the birth order, complete with times. Can you do the same?	6:00 Derec 6:10 Adele 0:10 later 6:40 Brand 0:30 later, 0:40 after Derec 7:30 Elena 0:50 later, 1:30 after Derec, 1:20 after Adele 7:50 Caleb 0:20 later, 1:50 after Derek, 1:40 after Adele, 1:10 after Brand. The missing interval is one hour. Method: Number the ten time points from 0 to 11 (6:00 to 7:50). The only ways to arrange them to get ten different intervals for the births are events at points 0, 1, 4, 9, and 11 and the reverse: 11, 10, 7, 2, and 0. The clue gives three birth times at 6:00, 6:10, and 7:50, so we have the first arrangement. The clues about alphabetic and reverse-alphabetic order giving five wrong placements mean that Caleb and Derek were not born 2nd, 3rd, or 4th; Adele and Elena were not born first or last, and Brand was not born 2nd or 4th. The 50-minute interval given at the end means puts Brand and Elena into the 3rd & 4th spots, which leaves 2nd as the place for Adele. Finally, we have Caleb and Derec to fill the first and last spots. Caleb and Nora share a birth position. The first paragraph mentions that Cogita is Nora's older sister, so Caleb cannot be the firstborn.	There is only one way (plus a mirror-image reflection) to arrange ten different intervals in a span of 11 ten-minute units. If you need help, search for "Optimal Rulers".	2.36	3.01	Math	F	2	5	4.9778	x	null	null	6:00 Derec 6:10 Adele 0:10 later 6:40 Brand 0:30 later, 0:40 after Derec 7:30 Elena 0:50 later, 1:30 after Derec, 1:20 after Adele 7:50 Caleb 0:20 later, 1:50 after Derek, 1:40 after Adele, 1:10 after Brand.
24	Unlucky Horse	Seven horses in a farm in Kentucky, Of three blacks, the oldest is a daddy; Of two browns, the 3 year old male is called BILLY, And the horse SNOWY is white as a lily. Of two half-sister mares, the black won in the Derby, She's a shade lighter than her daughter, BEAUTY; BEAUTY and her cousin LUCKY, both half the age of their auntie, But faster than either ROCKY or SUNNY. Three of the horses are ready for the Derby, A horse must be three years to be an entry; Maybe this year the farm gets lucky, Their stallion's loss last year was a pity. CHALLENGE: Describe the horse that lost in last year's Derby.	SNOWY, a 4 year old male white horse lost last year. The Derby is for three year old horses. Therefore only a current four year old horse could have lost last year. SNOWY is the only horse which could have been three last year (four this year). The farm is preparing three of the seven horses for this years Derby. There must therefore be at least three 3-year old horses among the seven. BILLY is 3-years old. Necessarily, BEAUTY and her cousin LUCKY must be 3 years old both. (They are of the same age). Beauty's mom could not be three because she won in the Derby before. The oldest black is even older than BEAUTY's mom. BEAUTY's aunt could not be three. If she were, then SNOWY must also be three to complete the three entries this year. This would mean that no horse would be four years old as BEAUTY and LUCKY would be one and a half years old. BEAUTY's mom won in the DERBY as a three year old, she could not win and lose at the same time. (The riddle suggests that the farm did not win last year so the mom must be over 5 years old). In sum, if BILLY, BEAUTY, and LUCKY are three years old, their aunt must be six. BEAUTY's mom must be five or more. The oldest black must be older than the black mom. Only SNOWY could be four this year. SNOWY is white (given), 4 years as deduced, and male from the fact that it was a stallion which lost last year. The names of BEAUTY's mom and aunt and that of the oldest black are immaterial. The same is true with the color of lucky.	For purposes of this riddle the following terms are defined as: Mare- female horse Stallion- mature male horse Derby- a race for three year old horses.	2.36	3.01	Pattern	null	x	x	x	x	null	null	SNOWY, a 4 year old male white horse lost last year.
25	More Mystery Numbers	There is a 10-digit number, represented by ABCDEFGHIJ, where each numeral, 0 through 9, is used once. Given the following clues, what is the number? 1) A + D = a square number 2) G + J = a triangle number 3) B + I = an even number 4) E * F = an odd number 5) C * H = a prime number 6) A / G = G / C 7) E + I = B + H	4615972308 For the product of two numbers to be a prime number (clue #5), one of those two numbers must be 1. Therefore, either C or H must be 1. To achieve the required proportion (clue #6), the numerals [AGC] must be one of the following combinations: 931 or 421 or 842. If [AGC] = 842, then D would have to be 1 (clue #1). Since either C or H must be 1, then D can not be 1. Since D can not be 1, then A can not be 8. Therefore, [AGC] can not be 842. The only remaining possibilities for [AGC] are 931 and 421. In either case, C = 1. If [AGC] = 931, then D must be either 0 or 7 (clue #1) and J must be either 0 or 7 (clue #2). Therefore, between them, D and J must use 0 and 7. E and F must both be odd (clue #4). However, four of the odd numerals would already be assigned (A = 9, G = 3, C = 1, either D or J = 7). Therefore, [AGC] can not be 931. This means that [AGC] must be 421. Therefore, A = 4 and G = 2. Since G = 2, then J = 8 (clue #2). J can not be 1 or 4, since those two numerals are now assigned. The only remaining letters that can be assigned to 6 are B and I. D can not be 6, as it would not produce a square number (clue #1). Neither E nor F can be 6, since that would not produce an odd number (clue #4). H can not be 6, as it would not produce a prime number (clue #5). Since either B or I must be 6, then 6 must be paired with 0 (clue #3), as the other even numerals have now been assigned. Since B and I share 0 and 6, then D = 5 (clue #1). Since B and I share 0 and 6, then E and H must also be separated by 6 (clue #7). The only remaining numerals that satisfy this requirement are 3 and 9. This means that F = 7. This sets H = 3 and E = 9, which then sets B = 6 and I = 0.	A triangle number can be expressed as the sum of the numbers 1 to n, for any integer value of n. Therefore the triangle numbers are 1, 3, 6, 10, 15, 21, 28, ...	2.22	3.01	Number	F	2	10	6.51401	7	null	null	4615972308
26	Alphabet Pyramids	Did you know that the mango is one of the world's most popular fruits? The mango is grown in North, South and Central America, the Caribbean, south and central Africa, as well as its native southern and south-east Asia. The mango is also packed with vitamins A, B and C. While eating a mango the other day, I started thinking about the ABC's. Then I remembered the set of 5-sided alphabet pyramids I had as a child. Here are some 5-letter words that can be spelled with just 5 of my pyramids: BELOW CANDY FORTY HELIX JABOT LEMON LIGHT MANGO OCHRE PEACH QUEST QUICK VIEUX Using these words, can you figure out which letters appear on each pyramid?	Let's start with the word MANGO, and assign a number to each pyramid. 1: M 2: A 3: N 4: G 5: O The word LEMON shares 3 letters with MANGO, so the L and E must go with the A and G, in some order. Because of the word PEACH, the E and A cannot be on the same pyramid, so the E must be on pyramid 4, while the L is on pyramid 2. Because of the word OCHRE, neither the C or H of PEACH can be on the same pyramid with the O, so the P must be on pyramid 5. Because of the word CANDY, the C cannot be on the same pyramid as the N, so it is with the M, leaving the H with the N. The Y cannot be with the O (FORTY), so it must be with the G, and the D is with the O. The R must then be on pyramid 2, to complete OCHRE. 1: M, C 2: A, L, R 3: N, H 4: G, E, Y 5: O, P, D The F and T of FORTY must be on pyramids 1 and 3, but the H and T cannot be on the same pyramid (LIGHT), so the T is on pyramid 1 and the F is on pyramid 3. This means that the I must be on pyramid 5, in order to complete LIGHT. 1: M, C, T 2: A, L, R 3: N, H, F 4: G, E, Y 5: O, P, D, I The J and B of JABOT must be on pyramids 3 and 4, but the B cannot be with the E, or else one cannot spell BELOW. Also, the W must be on pyramid 1. 1: M, C, T, W 2: A, L, R 3: N, H, F, B 4: G, E, Y, J 5: O, P, D, I The X in HELIX must be on pyramid 1, so we now have all the letters on that pyramid. There is only one letter left on pyramid 3, and it must be in VIEUX, QUEST and QUICK, so it must be the U. The V from VIEUX must therefore be on pyramid 2. The Q cannot be on the same pyramid as the I, in order to spell QUICK, so it is also on pyramid 2. The S cannot be on the same pyramid as the E (QUEST), so is therefore on pyramid 5, and the K is the last letter on pyramid 4. 1: M, C, T, W, X 2: A, L, R, V, Q 3: N, H, F, B, U 4: G, E, Y, J, K 5: O, P, D, I, S	Start with MANGO and LEMON; because they share three letters, you can start off with a pretty strong reduction and only have to consider how the other two pairs must be arranged	2.77	3	Clusters	F	5	5	14.1305	13	null	null	1: M, C, T, W, X 2: A, L, R, V, Q 3: N, H, F, B, U 4: G, E, Y, J, K 5: O, P, D, I, S
27	Petals Around the Rose	You roll five dice. The computer calculates the score. Your job is to find out what the computer based the score on. If you roll 5, 4, 6, 3, and 5, the score is 10. If you roll 1, 3, 3, 4, and 2, the score is 4. If you roll 1, 6, 2, 6, and 4,the score is 0. What is the method?	Only the dice that have a centre dot are counted (3 and five). Count the number of dots around the centre dot. These "petals" are the score. A five on the die gets a score of 4, and a three on the die gets a score of 2.	Think of the title. The score is never odd. Picture the dice in your head.	2.6	2.99	Pattern	A	x	x	x	x	null	null	Only the dice that have a centre dot are counted (3 and five). Count the number of dots around the centre dot. These "petals" are the score. A five on the die gets a score of 4, and a three on the die gets a score of 2.
28	On A Role	Carl, Draco, Emma, Ivy, June, & Xavior are playing a game with you in which you have to guess their roles in exactly 16 statements. The roles are: Normal - Has no abilities Liar - Knows all roles & has to lie Detective - Knows all roles Switcher - Switches 2 roles after the first statement (cannot switch themselves) Cupid - Pairs 2 players and lets them see each other's roles (cannot pair themselves) Spy - Knows who was switched The following 16 statements were made: Carl is not Cupid - June Ivy is the Liar - Carl I know someone's role - Draco I know the Switcher - Xavior Ivy is not Normal - Emma I wasn't switched - Ivy Emma knows Draco's role - June Xavior knows who was switched - Carl Emma & I are not the Spy - Draco Draco or June is Normal - Xavior I don't know the Spy - Emma I'm the Spy - Ivy The Cupid wasn't switched - June Xavior isn't Cupid - Carl I don't know the Detective - Draco I'm not the Spy - Xavior Who is who? *The Detective/Liar knows who was switched; if the Detective/Liar is switched then only the new Detective/Liar is updated	Normal=Draco Liar=Ivy Detective=Xavior Switcher=Emma Cupid=June Spy=Carl Explanation: Step 1: Draco, Xavior, & Emma are telling the truth "Ivy is the Liar - Carl" If Carl is telling the truth then Ivy is lying, otherwise Carl is lying Since Carl or Ivy is lying & there is only 1 liar, the other are honest Step 2: June is telling the truth (can't prove the 1st statement yet) "Ivy is the Liar - Carl" If Carl is telling the truth then Ivy is lying, if Carl is lying then Carl is lying However, since June is the 1st one to talk, June could have been swapped and started as the liar Step 3: Emma is paired "Emma knows Draco's role - June" This leaves 5 scenarios: 1. Emma is the Detective & is paired with June 2. June is Cupid & paired Draco & Emma 3. Emma is the Liar & is paired with June 4. Emma is the Liar & June is the Detective 5. June is lying Statements 3-5 can't be true since Emma & June are telling the truth; therefore Emma is paired with Draco or June Step 4: Emma isn't the Cupid or Normal "Cupid - Pairs 2 players and lets them see each other's roles (cannot pair themselves)" Cupid can't pair themselves "Draco or June is Normal - Xavior" Xavior is telling the truth; therefore Emma can't be Normal Step 5: Emma isn't the Detective or Spy: "I don't know the Spy - Emma" If Emma was the Detective or Spy, then Emma would know the Spy This leaves Emma with Switcher Step 6: June is Cupid & Draco is Paired "Emma knows Draco's role - June" We had 2 possible scenarios: 1. Emma is the Detective & is paired with June 2. June is Cupid & paired Draco & Emma However, Emma isn't the detective; therefore Draco & Emma are paired by June the Cupid Step 7: Draco = Normal "Draco or June is Normal - Xavior" June is Cupid & Xavior is telling the truth; therefore Draco is Normal Step 8: The final 3 "I'm not the Spy - Xavior" This leaves the Detective. "Xavior knows who was switched - Carl" This is true, which means Ivy is the liar & Carl is the Spy. Ivy & Carl were swapped	Step 1: Draco, Xavior, & Emma are telling the truth "Ivy is the Liar - Carl" If Carl is telling the truth then Ivy is lying, otherwise Carl is lying Since Carl or Ivy is lying & there is only 1 liar, the other are honest	2.53	2.99	Liars	G	2	6	2.85733	16	null	null	Normal=Draco Liar=Ivy Detective=Xavior Switcher=Emma Cupid=June Spy=Carl
29	Rags to Riches	One day, an eccentric billionaire decided to give a destitute man a break. But not a total break, as we shall see. So, he invites him into a room in his mansion with seven doors. There is also a large-screen projector that projects the following five images, repeatedly, one at a time: A human brain, Earth, the incomplete phrase: 'Fair and ____,' the letters AZCONMUT and a cheese sandwich on plain white bread with the edges perfectly cut off. The poor man was allowed an entire day to study the images, after which he would have to choose the door that corresponded to the commonality of the images. The next day the man walked through the correct door, and the billionaire made him rich. What door did the man choose?	The man chose door number FOUR. Here's why: The image of the human brain made the man think of 'four corners of the mind.' He recognized the capital letters AZCONMUT to be the abbreviations of the 'Four corner states' Arizona, Colorado, New Mexico, and Utah. He completed the phrase 'Fair and ____' with the word SQUARE, which also has also four corners. When he got hungry, he ordered the same sandwich in the last image. But instead of eating right away, he studied it, until he got the point that it too had four corners. Thus, the poor guy walked into a mansion poorer than poor, and walked out with a cheese sandwich, and enough dough to buy a small country. What he actually did with the money is anybody's guess.	Take a snack break, have one of the images.	2.8	2.97	Pattern	H	x	x	x	x	Y	null	Door four
30	Unlucky Car Thief	A car thief, who had managed to evade the authorities in the past, unknowingly took the automobile that belonged to Inspector Detweiler. The sleuth wasted no time and spared no effort in discovering and carefully examining the available clues. He was able to identify four suspects with certainty that one of them was the culprit. The four make the statements below. In total, six statements are true and six false. Suspect A: 1. C and I have met many times before today. 2. B is guilty. 3. The car thief did not know it was the Inspector's car. Suspect B: 1. D did not do it. 2. D's third statement is false. 3. I am innocent. Suspect C: 1. I have never met A before today. 2. B is not guilty. 3. D knows how to drive. Suspect D: 1. B's first statement is false. 2. I do not know how to drive. 3. A did it. Which one is the car thief?	Consider that six statements are false. A's first statement and C's first statement contradict each other. One of them is false. C's and D's contradict each other. One of them is false. Therefore, there are four additional false statements. Assume A is guilty. If so, A's second statement, B's second statement, and D's first statement are the additional false statements. Assume D is guilty. If so, A's second statement, B's first statement, and D's third statement are false. This also only makes five false statements. D did not do it. Assume C did it. If so, A's second statement, D's first and third statements are false. This again, makes only five false statements. After ruling out suspects A, C and D, B is the culprit. B's third statement, C's second statement, and D's first and third statements are the additional false statements. This adds up to six.	Consider that six statements are false. A's first statement and C's first statement contradict each other. One of them is false. C's and D's contradict each other. One of them is false. Therefore, there are four additional false statements.	2.58	2.96	Liars	H	2	4	0.60206	12	null	null	Suspect B
31	Class Photo 3	Stacey's class picture has 35 photos arranged in a 7 x 5 grid. The photos in the top row are numbered 1 through 7 from left to right, with the photos in the remaining rows similarly numbered. Given the following clues (bordering includes horizontal, vertical, and diagonal), where is Stacey's picture? X X X X X X X (1 - 7) X X X X X X X (8 - 14) X X X X X X X (15 - 21) X X X X X X X (22 - 28) X X X X X X X (29 - 35) 1) Stacey and her two best friends, Rhonda and Teresa, are located along a straight line (horizontally, vertically, or diagonally). However, Stacey does not border either Rhonda or Teresa. 2) The sum of the three positions (Stacey, Rhonda, and Teresa) is a prime number. 3) There are 18 boys and 17 girls. 4) Boys are not located at positions that are square numbers or cube numbers. 5) Girls are not located at positions that are prime numbers. 6) The sum of the positions where boys are located is less than the sum of the positions where girls are located. 7) There are no more than four girls in any row. 8) There are at least two girls in each column. 9) There are no more than three girls in any diagonal.	A) Boys are located at the following positions (clue 5): 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, and 31. Girls are located at the following positions (clue 4): 1, 4, 8, 9, 16, 25, and 27. B) A boy must be at position 33 (clue 9). Girls must be at positions 10, 24, 12, and 26 (clue 8). C) Boys must be at positions 14, 22, and 28 (clue 7). A boy must be at position 32 (clue 9). D) Two boys still need to be placed. To satisfy clue 9, they must be among the following three positions: 6, 18, and 30. The summation of all positions (1 through 35) is 630. To satisfy clue 6, the sum of the positions for boys must be less than one-half of 630, or less than 315. The 15 boys already placed have a position sum of 289. To satisfy clue 6, the remaining two boys must add no more than 25. This means that the last two boys must be placed at positions 6 and 18, producing a total of 313. Girls occupy the remaining positions (15, 20, 21, 30, 34, and 35). Step A Step B Step C Step D GBBGBxB GBBGBxB GBBGBxB GBBGBBB GGxBxBx GGGBGBx GGGBGBB GGGBGBB xGBxBxx xGBxBxx xGBxBxx GGBBBGG xBxGxGx xBGGGGx BBGGGGB BBGGGGB BxBxxxx BxBxBxx BxBBBxx BGBBBGG Stacey, Rhonda, and Teresa occupy positions that sum to a prime number (clue 1). The only sets of three positions that sum to a prime number are: 8, 9, 12 (sum 29) 9, 10, 12 (sum 31) Per clue 1, Stacey does not border either Rhonda or Teresa. With either set, Stacey is at position 12.	Boys are located at the following positions (clue 5): 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, and 31. Girls are located at the following positions (clue 4): 1, 4, 8, 9, 16, 25, and 27.	2.49	2.96	2D	H	3	35	12.4893	8	null	null	Position 12
32	5 Businessmen	These five businessmen represented different companies at a recent trade fair. Unfortunately, the hotel they were all due to stay in had accidentally double booked their rooms. They tried other hotels in the area, but all were fully booked. Consequently, they all agreed to share the only two rooms available in the hotel - one twin and one triple. From the clues, can you work out each man's name, company and official title? 1. When the five men realized their dilemma, they drew straws to see who would share with whom. The outcome for four of them was that the CEO shared with the businessman from ABM Inc. and Edgar shared with the Developer. 2. Alan does not work for Reed Right and is not the Director. The Director does not work for Lantel or Blue Teeth. 3. Neither Clarkson nor Grimaldi works for Reed Right. Grimaldi is either the IT Analyst or the CEO. 4. The businessman from Reed Right did not share a room with Thomas. 5. Clarkson, who does not work for Lantel, shared with either Thomas or Grimaldi but not both. 6. Edgar's surname is either Casson or Graves. Edgar did not share with Carl. 7. The businessman from Chiptech shared with the businessman from Lantel. 8. The CEO shared with the IT Analyst. 9. Casson works for either Blue Teeth or Chiptech. 10. Neither Joshua nor Alan works for ABM Inc. 11. Fielder shared with the Director. 12. The Accountant from Blue Teeth shared with the Developer. First names: Alan, Carl, Edgar, Joshua, Thomas. Last names: Casson, Clarkson, Fielder, Graves, Grimaldi. Company: ABM Inc., Blue Teeth, Chiptech, Lantel, Reed	First Name, Last Name, Company, Position: Carl Grimaldi, ABM Inc., IT Analyst Edgar Casson, Chiptech, Director Joshua Graves, Reed Right, CEO Alan Clarkson, Blue Teeth, Accountant Thomas Fielder, Lantel, Developer To solve this teaser, you first need to determine who shared which room with whom. Three delegates shared the triple and two shared the twin. The CEO shared with the businessman from ABM in one room and Edgar shared with the Developer in the other (1). Since Grimaldi is either the IT Analyst or the CEO (3) and the CEO shared with the IT Analyst, Grimaldi is in the same room as whoever is the CEO, IT Analyst and ABM delegate although Grimaldi could have been one of these people. Edgar did not share with Carl (6) so Carl is in the same bedroom as, and possibly is, the CEO, IT Analyst, Grimaldi and/or the ABM delegate. Grimaldi and Thomas were in different rooms so Thomas shared a room with Clarkson (5) and the Reed Right delegate was in a different room to Thomas. At this stage we know: Room 1 CEO IT Analyst ABM delegate Grimaldi Carl Reed Right delegate Room 2 Edgar Developer Thomas Clarkson Since the Chiptech delegate shared with the Lantel delegate (7), both of these must have been in room 2 otherwise there would be four delegates in room 1 which is not possible. Now this has been ascertained, the puzzle can be solved: The CEO shared with the IT Analyst so the IT Analyst must work for ABM (Clues 1 and 8) so the CEO must work for Reed Right. Since Grimaldi does not work for Reed Right, he must be the IT Analyst. Clarkson, Fielder and Casson are in room 2 so the CEO must be Graves. Graves is not Edgar (1), Thomas (4), Carl (IT Analyst) or Alan (2) so must be Joshua. Clarkson is not Thomas (5), Edgar (6), Carl or Joshua (in room 1) so must be Alan. The Director does not work for Lantel or Blue Teeth (2), Reed Right or ABM (room 1) so must work for Chiptech. This is not Graves or Grimaldi (room 1), Clarkson (2) or Fielder (11) so must be Casson. Since Graves; first name is Joshua, Casson must be Edgar (6). Alan Clarkson does not work for Reed Right or ABM (room 1); Lantel (5) or Chiptech so must work for Blue Teeth. Since he is not the Developer (12) he must be the Accountant. This leaves Thomas Fielder who is the Developer for Lantel.	To solve this teaser, you first need to determine who shared which room with whom	2.47	2.95	0D	G	3	5	4.1584	12	null	null	Carl Grimaldi, ABM Inc., IT Analyst Edgar Casson, Chiptech, Director Joshua Graves, Reed Right, CEO Alan Clarkson, Blue Teeth, Accountant Thomas Fielder, Lantel, Developer
33	Water Juggling	Here's what you have: -Two 8-liter jugs, filled with water -One 3-liter jug, empty -Four infinite size, empty pools Here's what your objective is: Fill each of the four pools with exactly 4 liters of water. Here are your constraints: -You have nothing else at your disposal. -There is no other water aside from the two 8-liter water filled jugs. -Once water is poured into any of the 4 pools it cannot be removed from there. -The jugs are not symmetric so you cannot measure amount by eye or judge based on shape.	It's not short but it's right - use a piece of paper and follow the steps using A, B, C and pools. Change the quantities in each as you complete each step - it is worth it to see it come out right. Lets label the jugs. Jug A - first 8-liter Jug B - second 8-liter Jug C - 3-liter. The four infinites are pool 1, pool 2, pool 3, and pool 4. 1. Jug A to Jug C 2. Jug C to pool 1 3. Jug A to Jug C 4. Jug A to pool 2 5. Jug C to Jug A 6. Jug B to Jug C 7. Jug C to Jug A 8. Jug B to Jug C 9. Jug C to Jug A At this point, we have: Jug A - 8 Jug B - 2 Jug C - 1 Pool 1 - 3 Pool 2 - 2 Pools 3&4 - empty 10. Jug C to pool 3 11. Jug B to Jug C 12. Jug A to Jug C 13. Jug C to Jug B 14. Jug A to Jug C 15. Jug C to Jug B 16. Jug A to Jug C 17. Jug A to pool 4 At this point, we have: Jug A - 0 Jug B - 6 Jug C - 3 Pool 1 - 3 Pool 2 - 2 Pool 3 - 1 Pool 4 - 1. 18. Jug C to Jug B 19. Jug C to pool 1 20. Jug B to Jug C 21. Jug C to pool 3 22. Jug B to Jug C 23. Jug C to pool 4 24. Jug B to pool 2 ... And we end up with the desired result: Jug A - 0 Jug B - 0 Jug C - 0 Pool 1 - 4 Pool 2 - 4 Pool 3 - 4 Pool 4 - 4 Tough, but workable.	I am not sure how to help you :). I solved this in 24 steps (you may have more or less). It helps to label the jugs and pools, and then draw. Oh, main key, try to work backwards, from filled pools, and see what final steps are even possible.	2.66	2.93	Algorithm	A	x	x	x	x	Measurement	null	1. Jug A to Jug C 2. Jug C to pool 1 3. Jug A to Jug C 4. Jug A to pool 2 5. Jug C to Jug A 6. Jug B to Jug C 7. Jug C to Jug A 8. Jug B to Jug C 9. Jug C to Jug A 10. Jug C to pool 3 11. Jug B to Jug C 12. Jug A to Jug C 13. Jug C to Jug B 14. Jug A to Jug C 15. Jug C to Jug B 16. Jug A to Jug C 17. Jug A to pool 4 18. Jug C to Jug B 19. Jug C to pool 1 20. Jug B to Jug C 21. Jug C to pool 3 22. Jug B to Jug C 23. Jug C to pool 4 24. Jug B to pool 2
34	Table Tennis Challenge	Patrice and seven of her friends organized the Ultimate Table Tennis Challenge to determine who the best Ping-Pong player among them was. The challenge consisted of three rounds of singles matches (two players competing per match). In each round, the first player to win FIVE games won the match and eliminated the opponent from the competition. The winners of the four first round matches advanced to the second round and the two second round winners advanced to the championship match. Each match was played at a different location, including the Beachcomber Swim Club. All first round matches were played on outdoor tables, both second round locations were indoor tables and the final round was played in the table tennis stadium at the New York Athletic Club. No two people won the same number of games, so players eliminated in the same round were ranked by the total number of games won. Identify each competitor's final ranking (first through eighth), full name (one last name is Chang), and the total number of games he or she won. In addition, figure out each location of each match, the competitors and their scores. 1. The winner of the match at the Southville YMCA lost at least three games on the indoor table in Uncle Phil's basement before meeting McNeilly in the finals. 2. The first round opponent of the eventual champion was neither Fitzroy (who lost in the first round) nor the person who lost at the Brooklyn Table Tennis Academy. 3. The championship round took the maximum possible number of games in a match. 4. The seven matches, in some order, were: Jamie's first round victory, the match in which White won exactly 2 games, the match at Eastlake Municipal Park, the match that Lottie lost, the only match Diaz played, the match Toskhaya lost and the match in which somebody won exactly one game. 5. Bill never played Dave. 6. Averson didn't play Jamie in the first round. 7. A total of 55 games were played in the whole challenge, 30 of which were the first round matches. 8. McNeilly, who isn't Lottie or Kristin, never played Samuel or Gianelli. 9. The four who advanced to the second round were: White, Lottie, the person who played Regina in the first round and someone whose indoor match was at the Islip Town Hall. 10. McNeilly's opponent in the first round won more games than Diaz. 11. Kristin never played at the Southville YMCA. 12. Regina won more games than the person eliminated at Eastlake Municipal Park. 13. Kristin won more games than Bill, who won at least five. 14. In the first round, Dave didn't play the eventual champion	RANKING/ PLAYER/ GAMES 1st - Jamie McNeilly, 15 games 2nd - Lottie Averson, 14 games 3rd - Kristin Toskhaya, 9 games 4th - Bill White, 7 games 5th - Patrice Chang, 4 games 6th - Regina Diaz, 3 games 7th - Samuel Fitzroy, 2 games 8th - Dave Gianelli, 1 game 1st Round Beachcomber, Jamie, 5, Patrice, 4 Brooklyn, Kristin, 5, Regina, 3 Eastlake, Bill, 5, Samuel, 2 Southville, Lottie, 5, Dave, 1 2nd Round Islip, Jamie, 5, Bill, 2 Uncle Phil's, Lottie, 5, Kristin, 4 3rd Round N. Y. Athletic, Jamie, 5, Lottie, 4 The final match was played at the New York Athletic Club (intro). The loser in the championship round lost 4 games (3) for a total of 9 games in the final round (intro and 3). There were 30 matches in the first round (7); with 20 of them being wins (intro) therefore the total of lost games in the first round are 10. From clue 4, we know that somebody won exactly 1 game. From the intro we know no one won the same number of games, therefore the number of games lost in the first round is 1, 2, 3, and 4, can't have 5 because that means they would have advanced to the next round. This leaves 55 (total games played (clue 7)) - 30 (1st round - clue 7) - 9 (Final round - clue 3) = 16 games in 2nd round. 10 of these 16 games are the winner's games, which leaves 6 games for the losers in round 2. The 2 loser's games can't be 3 & 3, because this would mean both players would have a total of 8 games each. No two players won the same number of games (intro). They can't be 5 & 1 because that would leave a tie and only 1 can advance. They can't be 6 & 0 because 5 wins advances someone, so no one can win 6. This leaves 2 & 4 as the games won by the losers in the second round. This means the total numbers of matches won from 1st ranked to 8th ranked are: 15, 14, 9, 7, 4, 3, 2 and 1 for a total off 55 games (7). From clue 1 we know that the Southville YMCA was used in round 1, Uncle Phil's Basement is used in round 2 and McNeilly is in the final game, which means McNeilly won a match in round 1 and in round 2 for a total of either 14 (if he loses the finals) or 15 (if he wins the finals) games. Islip Town Hall is used in the 2nd round (9), which leaves Eastlake Municipal Park, The Beachcomber Swim Club and Brooklyn Table Tennis Academy being used for the other 3 matches in the first round. From clue 9, we know the four first round winners are: White, Lottie, the one who played Regina in the first round and The Islip Town Hall match. McNeilly has to be 1 of these four (1). McNeilly isn't Lottie (8), can't be White since both are last names, so is either the one who played Regina or the one who played at Islip Town Hall. Regina lost the first round match (9). White is in the second round (9) and is the player who won only two games (4), which means White doesn't go to the finals and won a total of 7 games. From clue 4, four of the 1st round matches are: Jamie's 1st round victory, Eastlake Municipal Park (see above), the only match Diaz played and someone who won exactly one game. We know White won exactly two games (4) and the final round took the maximum number of games (3), therefore White's 2 game win has to be in the 2nd round. Since we now know the four 1st round matches, Toskhaya had to win in the 1st round and moves on to round 2. From clue 13, Bill won at least 5 games and Kristin won more than Bill. This means that both Bill and Kristin won their first round matches and moves on to the second round. The four players in round 2 are: Jamie, Lottie, Bill and Kristin. One of these four was the eventual winner, but it wasn't Bill (13) or Lottie (4), so Jamie or Kristin is the winner. Kristin isn't McNeilly (8) and never played at Southville (11), so she didn't play in the finals (1). This makes Jamie the winner. Since Bill didn't finish second overall (13 and above), he wasn't Jamie's opponent in the finals. Kristin wasn't in the finals (see above); therefore Lottie lost in the final match with a total of 14 games overall. Jamie and Lottie were the 2nd round winners. Lottie isn't McNeilly (8), therefore Jamie is, who won the final round. Lottie isn't Toskhaya (4) or White (9), therefore Lottie played against Toskhaya in round two. In the 1st round, Jamie McNeilly didn't play Fitzroy (2), Averson (6), Diaz (4) or Gianelli (8); thus he played Chang. Jamie didn't play at the Southville YMCA (1), Eastlake Park (4), Brooklyn Academy (2), thus he played on the Beachcomber Swim Club table in round one. Jamie didn't play Lottie, Kristin or Bill in round one, since they are winners in round one. Jamie didn't play Samuel (8) or Dave (14). From clue 9 Regina was the one who played Toskhaya in round one, therefore Jamie had to play Patrice in round 1. From clue 1 and above, we know Lottie played at the Southville YMCA in round one. From clue 13, Kristin won more games than Bill, so Kristin is Toskhaya and Bill is White. Regina didn't play at Eastlake (12) and she won more than one game, therefore she is Diaz. Regina Diaz didn't win overall 1 game (4); she won more than the Eastlake player (12) but less than McNeilly's first round opponent (10) -who is Patrice Chang. Thus, she won 3 games overall, the Eastlake opponent won 2 games overall and Patrice Chang won 4 games overall. Kristin didn't play at the Southville YMCA; therefore she played at the Brooklyn Academy. Lottie played Jamie in the final round, therefore her last name isn't Fitzroy (2) or Gianelli (8), therefore she is Averson. Lottie Averson played at Southville YMCA (1 and above). Bills 1st round opponent wasn't Dave (5), thus Lottie played Dave and Bill played Samuel in the 1st round. Samuel isn't Gianelli (8), thus he is Fitzroy and Dave is Gianelli.	Last names: Averson, Chang, Diaz, Fitzroy, Gianelli, McNeilly, Toskhaya and White	2.54	2.93	Tree	G	3	8	8.4141	14	null	null	1st - Jamie McNeilly, 15 games 2nd - Lottie Averson, 14 games 3rd - Kristin Toskhaya, 9 games 4th - Bill White, 7 games 5th - Patrice Chang, 4 games 6th - Regina Diaz, 3 games 7th - Samuel Fitzroy, 2 games 8th - Dave Gianelli, 1 game
35	Letter Blocks	A child has 4 blocks with a different letter on each side (no letter is repeated on different blocks either). If the list of words below can all be formed using these blocks, figure out which letters belong on which blocks... skid hoax joey glum rand grit monk fair vane wide cafe dupe joke bail shop	Block 1: S, E, M, B, R, X Block 2: K, W, Y, A, G, P Block 3: I, U, N, H, J, C Block 4: D, L, O, V, T, F	Look for pairs of words with lots of letters in common! Also consider letters which appear lots (like "e")	2.67	2.92	Clusters	F	7	4	13.495	15	null	null	Block 1: S, E, M, B, R, X Block 2: K, W, Y, A, G, P Block 3: I, U, N, H, J, C Block 4: D, L, O, V, T, F
36	Class Photo	Jacob's class picture has 40 photos arranged in a 8 x 5 grid. The photos in the top row are numbered 1 through 8 from left to right, with the photos in the remaining rows similarly numbered (as shown below). Given the following clues (bordering includes horizontal, vertical, and diagonal), where is Jacob's picture? X X X X X X X X (1 - 8) X X X X X X X X (9 - 16) X X X X X X X X (17 - 24) X X X X X X X X (25 - 32) X X X X X X X X (33 - 40) 1) There are 20 boys and 20 girls. 2) Each row and column has at least two girls, but no more than four girls. 3) Every girl borders at least one other girl. 4) Girls are located at positions that are prime numbers. 5) Boys are located at positions that are either squares or cubes. 6) Jacob is the only boy that borders a unique number of girls.	Per clue 4: girls are at positions 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and 37. Per clue 5: boys are at positions 1, 4, 9, 16, 25, 36, 8, and 27. B G G B G _ G B B _ G _ G _ _ B G _ G _ _ _ G _ B _ B _ G _ G _ _ _ _ B G _ _ _ Per clue 2: make sure each row/column has at least two, but no more than four, girls. This puts boys at positions 6 and 21, and a girl at position 33. B G G B G B G B B _ G _ G _ _ B G _ G _ B _ G _ B _ B _ G _ G _ G _ _ B G _ _ _ There are still seven girls to identify, which must be assigned to columns 2, 4, 6, and 8 (clues 1 and 2). This means that boys must fill the open spaces in the other columns (positions 15, 35, and 39). B G G B G B G B B _ G _ G _ B B G _ G _ B _ G _ B _ B _ G _ G _ G _ B B G _ B _ Since all girls must border at least one other girl (clue 3) and only one more girl can be added to column 2, the next placements can be made (girls at positions 14 and 26). B G G B G B G B B _ G _ G G B B G _ G _ B _ G _ B G B _ G _ G _ G _ B B G _ B _ The rest of column 2 must be boys (positions 10, 18, and 34). Because no row can have more than 4 girls, each row must have exactly 4 girls. Girls must then be at positions 12, 38, and 40. Boys must then be at positions 22 and 30. B G G B G B G B B B G G G G B B G B G _ B B G _ B G B _ G B G _ G B B B G G B G The final two girls must be at either positions 20/32 or 24/28 (clue 2). If the first combination is chosen, then there will be no boy that borders a unique number of girls (clue 6). By placing the girls at the second combination (and boys at the first combination), clue 6 will be satisfied. B G G B G B G B B B G G G G B B G B G B B B G G B G B G G B G B G B B B G G B G The boys in the first row border (1, 5, 4, 1) girls. The boys in the second row border (2, 5, 4, 3) girls. The boys in the third row border (4, 6, 5, 5) girls. The boys in the fourth row border (3, 3, 5, 4) girls. The boys in the fifth row border (2, 2, 3, 3) girls. The only boy that borders a unique number of girls is the boy who borders six girls, which is at position 20. Therefore, Jacob is at position 20.	The number 1 is not a prime number.	2.61	2.92	2D	null	3	40	12.4404	5	null	null	Position 20
37	Brown Eyes, Blue Eyes	On an otherwise deserted and isolated island, 200 perfect logicians are stranded. The islanders are perfectly logical in every decision they make, and they will not do anything unless they are absolutely certain of the outcome. However, they cannot communicate with each other. They are forbidden from speaking with one another, or signing, or writing messages in the sand, else they be smited by the god of the island. Of the 200 islanders, 100 have blue eyes, and 100 have brown eyes. However, no individual knows what color their own eyes are. There are no reflective surfaces on the island for the inhabitants to see a reflection of their own eyes. They can each see the 199 other islanders and their eye colors, but any given individual does not know if his or her own eyes are brown, blue, or perhaps another color entirely. And remember, they cannot communicate with each other in any way under penalty of death. Each night, when a ship comes, the islanders have a chance to leave the barren and desolate spit of land they have been marooned on. If an islander tells the captain of the ship the color of his or her own eyes, they may board the ship and leave. If they get it wrong, they will be shot dead. Now, there is one more person on the island: the guru, who the islanders know to always tell the truth. The guru has green eyes. One day, she stands up before all 200 islanders and says: "I see a person with blue eyes." Who leaves the island? And when do they leave?	All 100 blue-eyed people leave on the 100th night. First, we propose that two blue-eyed people are on the island. They would both leave on the second night, because they would each look at the other blue-eyed person on the second morning and realize that the only reason the other blue-eyed person wouldn't leave on the first night is because they see another person with blue eyes. Seeing no one else with blue eyes, each of these two people realize it must be them. Now consider the case of three blue-eyed islanders. It has been established that if only two people had blue eyes they would leave on the second night. You, the third blue-eyed person in our example, know this, as do the other two blue-eyed people. So when you wake up on the third morning, and the two other blue-eyed people have not left, you know that they must see another person with blue eyes, and you can see that no one else on the island has blue eyes, so you know it must be you. All three of you realize this simultaneously, and all three leave on the third night. If a fourth blue-eyed person is on the island, he will reason the scenario with three blue-eyed people on the island, and when he sees that they have not left the island during the fourth morning, he/she/it will leave the island on the fourth day, and so will all the other blue-eyed people. If we follow this pattern, we will eventually reach the answer of 100 people leaving the island after 100 days.	What would happen if there was only one blue-eyed person on the island and the rest of the islanders were brown-eyed? What about two? What about three?	3.16	2.91	Algorithm	H	x	x	x	x	Communication	null	All 100 blue-eyed people leave on the 100th night.
38	Breaking the Billiard Ball	It is your task to determine how high you can drop a billiard ball without it breaking. There is a 100 story building and you must determine which is the highest floor you can drop a ball from without it breaking. You have only two billiard balls to use as test objects. If both of them break before you determine the answer then you have failed at your task. What is the order of floors that you should drop the balls from to minimize the number of droppings that you will have to make to determine the answer? Assume that if a ball doesn't break you can reuse it without worrying about it being weakened.	If the proper order is chosen, you can determine the breaking point with a maximum of 14 drops. Here's how to do it: First drop the first ball from the 14th floor. If it breaks you can determine the exact breaking point with the other ball in at most 13 more droppings, starting at the bottom and going up one floor at a time. If the first ball survives the 14 floor drop then drop it again from the 27th (14+13) floor. If it breaks you can determine the exact breaking point with at most 12 more droppings. If the first ball survives the 27 floor drop then drop it again from the 39th (14+13+12) floor. If it breaks you can determine the exact breaking point with at most 11 more droppings. Keep repeating this process always going up one less floor than the last dropping until the first ball breaks. If it breaks on the xth dropping you will only need at most 14-x more droppings with the second ball to find the breaking point. By the 11th dropping of the first ball, if you get that far, you will have reached the 99th floor.	When you have one ball remaining, the strategy to find the desired height is clear. Then consider how many tries this will take conditioned on when the first ball breaks (and you then have one ball remaining)	2.81	2.91	Algorithm	A	x	x	x	x	Measurement	null	If the proper order is chosen, you can determine the breaking point with a maximum of 14 drops. Here's how to do it: First drop the first ball from the 14th floor. If it breaks you can determine the exact breaking point with the other ball in at most 13 more droppings, starting at the bottom and going up one floor at a time. If the first ball survives the 14 floor drop then drop it again from the 27th (14+13) floor. If it breaks you can determine the exact breaking point with at most 12 more droppings. If the first ball survives the 27 floor drop then drop it again from the 39th (14+13+12) floor. If it breaks you can determine the exact breaking point with at most 11 more droppings. Keep repeating this process always going up one less floor than the last dropping until the first ball breaks. If it breaks on the xth dropping you will only need at most 14-x more droppings with the second ball to find the breaking point. By the 11th dropping of the first ball, if you get that far, you will have reached the 99th floor.
39	If There's a Camel	Every year during his birthday, the Sultan sponsors 3 camel races with the following prizes (listed in order 1st, 2nd, 3rd): RACE A $500 300 100 RACE B $250 150 75 RACE C $150 100 50 $500 bonus for winning all 3 Races. (SLAM) $200 bonus for winning 1st, 2nd, and 3rd in any one Race (SWEEP). ALI BOBO tells you that he owns the 3rd ("Aluminum"), 6th("Boron"), and 9th("Copper") fastest camels. He concedes that KAREEM owns the 1st, 4th, and 7th fastest camels, while SHARIF has the 2nd, 5th, and 8th fastest entries. There are other owners but with far inferior camels. The Rules a. Maximum 3 camels per owner. b. A camel can run only in one race. c. An owner may enter his camels all in one race or distribute them as he desires. Last year ALI BOBO's camels won third place in each of the 3 Races. His gross winnings amounted to $225. ALI BOBO wants a risk-free strategy to increase his total winnings. QUESTION: What should be ALI BOBO's strategy?	Ali Bobo must enter Copper in Race A, Aluminum in Race B, and Boron in Race C. SCENARIOS 1. Kareem defends his Slam and fields his camels in RACES A,B, and C according to their speed. Shariff follows that same strategy. ALI's Aluminum will win in Race B over the K(4th) and S(5th). Boron will win in Race C over K(7th) and S(8th). Copper will still place 3rd in Race A. Total Winnings $500. 2. Kareem defends his SLAM. Shariff follows Ali's strategy. Aluminum will place second to S(2nd) in Race B. Boron will place second to S(5th) in Race C. Copper will place third to K(1st) and S(8th). Total winnings: $350. 3. Kareem loses his mind and does not go for the grand slam. He enters his 3 camels in Race A. Shariff follows his strategy in Scenario 1. Copper will not win anything in Race A. Aluminum will win in Race B. Boron will win in Race C. Winnings: $400. 4. Same as Scenario 3 but Shariff has same strategy as Ali. Copper loses in Race A. Aluminum places second in Race B. Boron places second in Race C. Winnings $250. 5. Kareem camels all in Race A. Shariff's all in race B. Copper loses in Race A. Aluminum still places second in Race B. Boron wins in Race C. Winnings $300. 6. Kareem defends his slam. Shariff camels all in race B. Copper will place second in Race A. Aluminum will still be second in Race B. Boron will win over K(7th) Winnings:$600. 7. Kareem and Shariff has same strategy as Ali. Copper will be third, Aluminum will be third. Boron will be third. Winnings:$225. Same as last year. There are other scenarios but with the strategy with the worst case scenario for Ali is $225.	Sometimes we must sacrifice some battles to win the war.	2.49	2.91	Math	F	x	x	x	x	null	null	Ali Bobo must enter Copper in Race A, Aluminum in Race B, and Boron in Race C.
40	Twins and Their Mistakes	Six sets of twins ( a boy and a girl in every case) made several errors in their history and geography examinations; and it was noted that every girl made precisely the same number of errors as her brother in the two subjects. Name each pair of siblings and their surname and work out how many mistakes each made in their history and geography examination papers. 1. The boy (not Luke) whose sister is Louella made more history errors than Sammy. 2. George did better in history than the boy surnamed O'Connell, who made either one more or one less geography error than the twins surnamed Dean. 3. Anne made either one more or one less geography error than Louella. 4. The twins who made 11 geography errors didn't make exactly 11 history errors. 5. David and his sister made either one more or one less mistake in the history exam than the twins who made 14 geography errors. 6. Edward and his sister did worse at history than the pair who made 15 geography errors. Edward made one more error in the geography exam than Luke. 7. The McCall twins didn't make one less history mistake than the Vole twins. 8. Susan (who made seven history errors) made one less geography error than the girl who made one less history error than Anne. 9. The twins surnamed Waters made one more history mistake than the twins surnamed Seal, who made more geography errors than the McCall twins. 10. Gail made one more geography error than the girl who made one more history error than Louella. 11. Martin made either one more or one less geography error than his best friend and his sister, who made more history mistakes than Diane. 12. Wendy and her brother (who didn't make eight history mistakes) didn't make as many errors in geography as George and his sister. Brothers are David, Edward, George, Luke, Martin & Sammy. Sisters are Anne, Diane, Gail, Louella, Susan & Wendy. Surnames are Dean, McCall, O'Connell, Seal, Vole & Waters. Geography errors are 10, 11, 12, 14, 15 & 16. History errors are 6, 7, 8, 10, 11 & 12.	Susan made seven history errors (clue 8) and no one made nine, so Anne made either 11 or 12. Louella didn't make six history errors (1), so (10) must have made either 10 or 11. If Louella made 11 and Anne made 12, then Susan made one less geography error than Louella (8) and Gail made one more than Anne (10). But then, since no one made 13 geography errors, clue 3 doesn't work. So Louella made 10 history errors. If Anne made 11 history errors, then Gail made one more geography error than Anne (10) and Susan made one less geography error than Louella (8). But again, since no one made 13 geography errors, clue 3 still doesn't work. So Anne made 12 history errors. The twins with 11 errors made one more geography error than Susan (8) and one less than Gail (10), so Gail made 12 or 16 geography errors and Susan made 10 or 14 : while twins with 11 history errors made 11 or 15 geography errors. Thus those with 11 history errors made 15 geography errors (4), Gail made 16 geography errors and Susan made 14. Edward made 12 history errors (6) so is Anne's brother; Anne and her brother made either 10, 11 or 12 geography errors, so (6) made 11 or 12 and Luke and his sister made 10 or 11, ie one of them made 11. Luke's sister isn't Louella (1), so Luke made either six or eight history errors, as did David (5). Thus David's sister is Gail. Anne made 11 geography errors (3), so Luke made 10 and Louella made 12. Sammy's sister is Susan (1). Wendy made 10 geography errors (12), so Diane made 15. Luke (who is Wendy's brother) made six history errors (12), so David made eight. By elimination, Sammy made seven and so is Susan's brother. Martin's sister is Louella (11). Diane's brother is George. Edwards is surnamed O'Connell (2) and the Dean girl is either Louella or Wendy (10 or 12 geography errors). The Waters and Seal twins (9) made either eight and seven history errors or else 11 and 10; so the Seal twins made 14 or 12 geography errors and the McCall twins made 10 or 12. If the Seal twins made 12 geography errors and the McCall twins made 10, then (above) the Dean twins are excluded. Thus Sammy's surname is Seal and David's is Waters. Diane's surname is Vole. Martin's isn't McCall (7), so must be Dean. Luke's is McCall. Thus ( geography-history ); David - Gail - Waters - 16 -8; Edward - Anne - O'Connell - 11- 12; George - Diane - Vole - 15 - 11; Luke - Wendy - McCall - 10 - 6; Martin - Louella - Dean - 12 - 10; Sammy - Susan - Seal - 14 - 7;	Susan made seven history errors (clue 8) and no one made nine, so Anne made either 11 or 12.	2.47	2.91	0D	F	5	6	11.4293	12	null	null	David - Gail - Waters - 16 -8; Edward - Anne - O'Connell - 11- 12; George - Diane - Vole - 15 - 11; Luke - Wendy - McCall - 10 - 6; Martin - Louella - Dean - 12 - 10; Sammy - Susan - Seal - 14 - 7;
41	The Dwarvish Feast	In a forest somewhere in Scotland lives a group of 100 dwarves. Each night they meet in the middle of the forest for a grand feast. When morning comes, they all go home. Each dwarf is wearing either a red hat or a blue hat. Curiously, there are no mirrors in the forest, so no dwarf knows the color of his own hat. A dwarf would never take off his hat to see its color, and a major dwarf faux pas is to comment on the color of another dwarf's hat. The dwarves know, however, that there is at least one red hatted dwarf and one blue hatted dwarf. One day, the master dwarf announces that the nightly feast will only be intended for blue hatted dwarves, and as soon as a dwarf knows that he is wearing a red hat, he should not come back the next day, and he should never return. How many days does it take before there are no dwarves left with red hats at the party? (Assume all the dwarves are equally capable of figuring it out, in other words, there are no smart dwarves, and no stupid dwarves...)	It will take one more day than the number of dwarves with red hats. How this works is: assume that there is only one red-hatted dwarf. He would go to the party only to see 99 blue hats. He knows that there is at least one red hat. Since all he sees is blue, he knows it must be him, so he knows not to come back the next day. Meanwhile, the blue hatted dwarves can only see one red hat, so they think that if he comes back tomorrow, then he must have seen another red hat. Since each blue hatted dwarf only sees one red hat, he would assume that if the red hatted dwarf came back tomorrow, then he must be the other red hat that the first red hatted dwarf saw. So the second day, all the blue hatted dwarves would come expecting to see if the red hatted dwarf came back. Which he wouldn't, because he knows he has a red hat. So the first day there are no dwarves with red hats is day 2, or one day more than the number of dwarves with red hats. If there were two dwarves with red hats, each red hatted dwarf would realize on the second day that he was wearing a red hat, because he would see that the other red hat had come back, and that means that he must have seen another red hat. Since the red hats would see 98 blue hats, they would know on the second day, and the third day would be the first day that no red hatted dwarves came to the feast. This same system works for any number of red hats, because each time a blue hatted dwarf is thinking that if the red hats come back tomorrow, then he must have a red hat, the red hatted dwarves already know, and so they don't come the next day.	The number of days depends on the number of red hats.	2.33	2.89	Algorithm	H	x	x	x	x	Communication	null	It will take one more day than the number of dwarves with red hats.
42	Military Fun 3	Please do Military Fun and Military Fun 2 first before doing this teaser. This teaser continues on from the first and second times the friends got together, and will give away the answer to Military Fun and Military Fun 2. So, please do those teasers first. This time the same 10 friends are going to go through a training camp so that they can be ready for their next pretend battle. More friends are finding out about this military fun and want to join, Private Brianna and Private Ben have come into this group too. Today the friends will be running 3 laps around the park. At the end of the race, the friends will move up or down in ranks according on how they did. If you can't move up or down any ranks, you will stay in the same rank that you are currently in. The scoring will be as follows 1st Place- Move up 5 ranks 2nd Place- Move up 4 ranks 3rd Place- Move up 3 ranks 4th and 5th Places- Move up 1 rank each 6th and 7th Places- Stay the same rank 8th and 9th Places- Move down 1 rank each 10th and 11th Places- Move down 2 ranks each 12th Place- Move down 3 ranks The ranks people have right now: Lieutenant General Stephen Colonel Anna Major Felicia Captain Clark Sergeant Abby Sergeant Brad Corporal Jessica Private Paul Private Kelsey Private Luke Private Brianna Private Ben This is a list of the ranks again, just in case anyone forgot it. Ranks 1. Lieutenant General 2. Brigadier General 3. Colonel 4. Lieutenant Colonel 5. Major 6. Captain 7. First Lieutenant 8. Second Lieutenant 9. First Sergeant 10. Sergeant 11. Corporal 12. Private The First Lap: Stephen, Ben, Paul, and Jessica took off sprinting taking the top 4 spots. Felicia and Brianna aren't far behind though. Kelsey, Anna and Abby were bringing up the back as they had a late start. In the top 4 runners, the bottom two ranked people were doing the best and the top ranked person was doing the worst. The Major was in 6th place as Brianna passed her for 5th. Luke was just about to pass Felicia, but tripped and fell back to 9th place as Clark and Brad passed him in that order. The back three girls were in their places according to their rank, the highest rank being 10th place and the lowest rank being 12th place. The Second Lap: Paul slipped on a water puddle and fell back to third place, leaving the person he was right by, way in front. Clark moved up 2 spots, pushing those two people back one place each. Then, Felicia and Anna switched places, and Luke and Brad switched places. The people in 11th and 12th ended up switching places just before the third lap as well. The Third Lap: The two people in 10th and 11th place switched spots, the two people in 5th and 6th places switched spots, and the two people in 7th and 8th places switched spots. Brad ended up getting passed by the two people directly behind him, and Jessica was passed by the person directly behind her. Everyone then finished in the order that they are currently in. Can you figure out which place everyone is in, and what rank they will be after this race?	The Order the finished in was: Ben, Paul, Jessica, Stephen, Brianna, Clark, Luke, Anna, Kelsey, Felicia, Brad, Abby. Here is how they got there: On the first lap the top 4 runners were Stephen, Ben, Paul, and Jessica. Felicia and Brianna weren't far behind which means they were in 5th and 6th place. With Kelsey, Anna, and Abby in the back (10th, 11th, and 12th places), that means Luke, Brad, and Clark were in 7th, 8th, and 9th. In the top 4 runners, the bottom two ranked people are Ben and Paul, which means that they were in 1st and 2nd, and the top ranked person was doing the worst, Stephen, which means that he was in 4th putting Jessica in 3rd place. Brianna was in 5th place, and Major Felicia was in 6th place. Clark and Brad passed Luke in a certain order, making Clark 7th, Brad 8th, and Luke 9th. The three girls in back then were in their places according to their rank, so that put Anna in 10th, Abby in 11th, and Kelsey in 12th. So, now we know what place everyone is after this lap. On the second lap Paul slipped and was passed by Jessica, putting Ben in 1st, Jessica in 2nd, and Paul in 3rd. Clark moved up 2 spots putting him in 5th place, Brianna in 6th place, and Felicia in 7th place. Felicia then switched places with Anna, which put Felicia in 10th place, and Anna in 7th place. Luke and Brad switched places as well, which put Luke in 8th, and Brad in 9th. The 11th and 12th place people switched places too, which put Kelsey in 11th, and Abby in 12th. On the third lap the 10th and 11th place people switched spots, putting Kelsey in 10th, and Felicia in 11th. 5th and 6th place switched, making Brianna in 5th, and Clark in 6th, and the 7th and 8th place people switched, putting Luke in 7th and Anna in 8th. Brad was passed by the two people who were directly behind him which made Kelsey in 9th, Felicia in 10th, and Brad in 11th. Jessica was also passed by Paul, the person directly behind her, putting Paul in 2nd, and Jessica in 3rd. Their new ranks are: Lieutenant General Stephen Lieutenant Colonel Anna Captain Clark First Lieutenant Ben First Lieutenant Felicia Second Lieutenant Jessica Second Lieutenant Paul Corporal Brianna Private Luke Private Kelsey Private Brad Private Abby	On the first lap the top 4 runners were Stephen, Ben, Paul, and Jessica. Felicia and Brianna weren't far behind which means they were in 5th and 6th place. With Kelsey, Anna, and Abby in the back (10th, 11th, and 12th places), that means Luke, Brad, and Clark were in 7th, 8th, and 9th.	2.22	2.89	Algorithm	null	x	x	x	x	Instructions	null	The Order the finished in was: Ben, Paul, Jessica, Stephen, Brianna, Clark, Luke, Anna, Kelsey, Felicia, Brad, Abby. Their new ranks are: Lieutenant General Stephen Lieutenant Colonel Anna Captain Clark First Lieutenant Ben First Lieutenant Felicia Second Lieutenant Jessica Second Lieutenant Paul Corporal Brianna Private Luke Private Kelsey Private Brad Private Abby
43	Numberrangements	In Numberrangements, you are given an arrangement of letters. The letters represent all of the whole numbers from 1 to the total number of letters used. Each letter represents a different number. Using the clues given, find which number each letter represents. ABC DEF GHI 1. The sum of the top row is greater than the sum of the middle row, which is greater than the sum of the bottom row. 2. E is a prime factor of G. 3. F is greater than A. 4. The sum of B and G is equal to H. 5. I is not 1.	A=7, B=1, C=9 D=6, E=2, F=8 G=4, H=5, I=3 From Clue 2, E must be 2, 3, 5, or 7, but it cannot be 5 or 7 because that would force G to be a greater multiple of 5 or 7, and only the numbers 1 to 9 are used. E must be 2 or 3 and G must be 4, 6, 8, or 9. Let's try I=2. In that case, E=3 and G=6. H must be greater than 6 because of Clue 4. The most G+H+I can be is 14 because of Clue 1, since the sum of all nine numbers is only 45. So, I cannot be 2, and it therefore must be at least 3 because of Clue 5. If I=4, then G cannot be 4, and must be 6, 8, or 9. Again, since H must be greater than G, the bottom row's sum will be too high. If I = 5, then the minimums for G and H would be 4 and 6, respectively -- a sum of 15. If I = 6, then the minimum sum again is 15. This means I MUST be 3, which forces E=2 and G=4, 6, or 8. If G is 6 or 8, the sum of the bottom row will be too great, so G=4. The greatest that H can be is 7, which also means that B can only be 1, 2, or 3, from Clue 4. But 2 and 3 are already used, so B=1 and H=5. This leaves A, C, D, and F, to be paired with 6, 7, 8, and 9, in some order. We know from Clue 1 that A+B+C > D+E+F, but E is already 1 greater than B, and from Clue 3, we know that F > A. This means that C must be at least 3 greater than D to make up for the top row trailing by at least 2. So, C must be 9, and D must be 6. This leaves 7 and 8 to be A and F, so of course, F=8 and A=7.	Start with casework on clue 2.	2.86	2.88	Number	F	2	9	5.5598	5	2D	null	A=7, B=1, C=9 D=6, E=2, F=8 G=4, H=5, I=3
44	Opposites 22	In the following code, each symbol stands for one of five letters. ! stands for T, E, O, Z, or Y ? stands for F, G, A, Q, or I # stands for N, I, W, A, or U $ stands for T, E, N, I, or H < stands for R, C, A, S, or B * stands for I, D, E, U, or S & stands for J, I, E, P, or K ^ stands for O, L, G, I, or H > stands for L, S, N, C, or E The nine letter code word, <$^&?*!#>, can be translated into two English words that are opposites. What are the two words?	Religious and Atheistic.	Belief	2.62	2.87	Linguistic	F	2	9	12.2804	1	null	null	Religious and Atheistic.
45	U.N.K.A.L	MADADIA has been chosen to host the latest United Nations Kebab Annual Liaisons (U.N.K.A.L). Madadia's mayoress, Madka Owdiseez, has invited several wives of delegates of UNKAL for an informal luncheon. She plans to seat her 9 guests in a row such that each lady will be able to converse with the person directly to her left and right. She has prepared the following list. Mrs. F speaks English only. Mrs. G speaks English and French. Mrs. H speaks English and Russian. Mrs. J speaks Russian only. Mrs. K speaks English only. Mrs. L speaks French only. Mrs. M speaks French and German. Mrs. N speaks English and German. Mrs. O speaks English only. How many distinct seating arrangements are possible? Give all possible seating arrangements. Bear in mind that Madka Owdiseez is not one of the 9 to be seated in a row. Note that ABCD and DCBA are the same	With each arrangement considered identical to its reverse, there are 126 possible arrangements. FKO are interchangeable, and can be arranged 6 ways. FKO stays together unless N is next to M outside GLM (more on that below). JH must be together, and J must be at the end, because H is the only other Russian speaker. JH has 2 slots in the above configuration (H next to FKO, with J on the outside). GLM has 1 slot in the above configuration (G next to FKO, opposite JH). 2[JH]6[FKO]1[MLG]=12 arrangements, or 2 mirror groups of 6 arrangements each. Thus, 6 distinct arrangements - 1 for each FKO order. Keeping the above groups self-contained, N has 5 slots (2 within FKO, 1 between FKO and H, 1 between FKO and G, 1 beside M). That makes 30 arrangements - 5 for each FKO order. When N is in certain positions, however, the groups can break up. Unless N is next to M outside GLM, GLM can be GML. If N is between FKO and GLM, GLM can scramble, and G can be anywhere touching FKO, except N cannot touch L. When G-[L/M]-N are consecutive in either direction, FKO can straddle that subgroup. That makes 126 arrangements - 21 for each FKO order. Here are the 21 arrangements, using xxx for the interchangeable FKO. JHNxxxGLM, JHNxxxGML, JHxNxxGLM, JHxNxxGML JHxxNxGLM, JHxxNxGML, JHxxxNGLM, JHxxxNGML JHxxxNMGL, JHxxxNMLG, JHxxNMLGx, JHxNMLGxx JHNMLGxxx, JHxxxGLMN, JHxxGLMNx, JHxGLMNxx JHGLMNxxx, JHGxxxNML, JHxGxxNML, JHxxGxNML JHxxxGNML Apply each FKO order - F-K-O, F-O-K, K-F-O, K-O-F, O-F-K, O-K-F - to each xxx above. That makes 21*6=126 arrangements.	FKO are interchangeable, and can be arranged 6 ways. FKO stays together unless N is next to M outside GLM (more on that below).	2.29	2.87	Math	F	x	x	x	x	null	null	Here are the 21 arrangements, using xxx for the interchangeable FKO. JHNxxxGLM, JHNxxxGML, JHxNxxGLM, JHxNxxGML JHxxNxGLM, JHxxNxGML, JHxxxNGLM, JHxxxNGML JHxxxNMGL, JHxxxNMLG, JHxxNMLGx, JHxNMLGxx JHNMLGxxx, JHxxxGLMN, JHxxGLMNx, JHxGLMNxx JHGLMNxxx, JHGxxxNML, JHxGxxNML, JHxxGxNML JHxxxGNML Apply each FKO order - F-K-O, F-O-K, K-F-O, K-O-F, O-F-K, O-K-F - to each xxx above. That makes 21*6=126 arrangements.
46	Countries of the World	A man named Stewart is traveling all over the world. First he travels to Cape Town in South Africa. Then to Jakarta in Indonesia. Then to Canberra in Australia. Then to Rome in Italy. Then to Panama City in Panama. Where does he travel next?	Santiago in Chile. He travels to each continent in alphabetical order then to the capital of the country that has the most southern latitude.	Each time he travels to a continent he has not traveled to.	2.25	2.87	Pattern	H	x	x	x	x	null	null	Santiago in Chile.
47	Alien Ambassadors	The boffins from NASA have received and decoded a digital message from the Galactic Council, informing them that four alien ambassadors from the solar system are due to visit Earth in the next 24 hours. The aliens are Agurgle from Uranus, Wym-Inar from Venus, ChimChim from Pluto and Mr. Arthur Johnson from Saturn. 24 hours later, they receive a mystery message saying that if any alien comes off the ship that is green, tentacled and slimy, then they are actually an undercover assassin from Neptune. By then, however, the aliens have all landed and are in adjacent decontamination booths, waiting to be let in to NASA Headquarters. One alien turns out to be green, tentacled and slimy! From the clues below, who is the Neptunian Assassin? 1) Wym-Inar from Venus is the only ambassador in a booth next to exactly one tentacled alien. 2). Two of the ambassadors who are not green, are each in booths next to Agurgle from Uranus. 3) ChimChim from Pluto is the only ambassador not in a booth next to exactly one Un-slimy alien. Who do the NASA boffins not let out of the booth?	ChimChim from Pluto is green, tentacled and slimy and so, is the Assassin. Looking at clue 2 we know that both the ambassadors standing next to Agurgle from Uranus are not green. Also, from the body of the teaser, we also know only one alien is green, tentacled and slimy. So there are two deductions to be made: (Note the key is - Alien (Green, Tentacled, Un-Slimey). Where "Y" stands for Yes and "N" stands for No. "?" denotes unknown, and each set of braces[] indicates a booth) Either Deduction A [ N, ?, ?] [Agurgle from Uranus Y, Y, N] [ N, ?, ?] [ ?, ?, ?] Or Deduction B [N, ?, ?] [Agurgle from Uranus ?, ?, ?][ N, ?, ?] [Y, Y, N] You can see that either Agurgle from Uranus or the alien at the extreme right hand booth is green, tentacled and slimy. Now taking clue 3, you can work out that ChimChim from Pluto's booth is next to a slimy alien AND each of the other aliens' booths are next to precisely one slimy alien. So, based on the first set of deductions, you can infer the following. Deduction A (ii): [ChimChim from Pluto N, ?, N] [Agurgle from Uranus Y, Y, N] [N, ?, Y] [?, ?, Y] Or Deduction B (ii): [N, ?, Y] [Agurgle from Uranus ?, ?, Y][ N, ?, N] [ChimChim from Pluto Y, Y, N] You can then use clue 1 to eliminate one of these deductions: Wym-Inar from Venus is the only alien in a booth next to exactly one tentacled alien. But in Deduction A(ii), ChimChim from Pluto's booth is next to exactly one tentacled alien. Therefore, Deduction A (ii) is not possible and Deduction B (ii) is the correct one. Deduction B (ii): [N, ?, Y] [Agurgle from Uranus ?, ?, Y][ N, ?, N] [ChimChim from Pluto Y, Y, N] So, looking again at clues 2 and 3, there are a further 2 possible deductions to be made. Deduction A (iii) [Mr. Arthur Johnson from Saturn N, N, Y] [Agurgle from Uranus] [?, N, Y] [Wym-Inar from Venus N, N, N][ChimChim from Pluto Y, Y, N] Deduction B (iii) [Wym-Inar from Venus N, N, Y][Agurgle from Uranus ?, Y, Y][Mr. Arthur Johnson from Saturn N, N, N][ChimChim from Pluto Y, Y, N] So, ChimChim from Pluto is green, tentacled and slimy, and is therefore our Neptunian Assassin.	Don't get too confused with the Un-slimy bit.	2.23	2.87	0D	H	5	4	4.9926	3	Traits	null	ChimChim
48	Kebab Line Up	Four men are in a line at the Madadian Police station, charged with unlicensed kebab breeding. The men are Mad Ade, Buster Artery, Cliff Hedge and Donny Moe - and they are standing in a straight line. One man is fair, handsome and unscarred. Two men who are not fair, are each standing next to Mad Ade Buster Artery is the only man standing next to exactly one handsome man. Cliff Hedge is the only man not standing next to exactly one scarred man. Who is fair, handsome and unscarred?	Cliff Hedge is fair, handsome and unscarred. From (2), both the men standing next to Mad Ade are not fair. Also, exactly one man is fair, handsome and unscarred. Hence, there are two cases: Case 1 :: ? (N, ?, ?) : Mad Ade (Y, Y, N) : ? (N, ?, ?) : ? (?, ?, ?) Case 2 :: ? (N, ?, ?) : Mad Ade (?, ?, ?) : ? (N, ?, ?) : ? (Y, Y, N) Note the representation - Name (Fair, Handsome, Scarred). "Y" stands for Yes and "N" stands for No. Mad Ade (Y, Y, N) means Mad Ade is Fair, Handsome and Unscarred.(oh, how true this is..NOT) It is clear that either Mad Ade or the man at the extreme right is fair, handsome and unscarred. From (4), it is deduced that Cliff Hedge is standing next to unscarred man and each of the other men standing next to exactly one scarred man. Case 1 :: Cliff Hedge (N, ?, N) : Mad Ade (Y, Y, N) : ? (N, ?, Y) : ? (?, ?, Y) Case 2 :: ? (N, ?, Y) : Mad Ade (?, ?, Y) : ? (N, ?, N) : Cliff Hedge (Y, Y, N) From (3), Buster Artery is the only man standing next to exactly one handsome man. But in Case 1, Cliff Hedge is standing next to exactly one handsome man. Hence, Case 1 is not possible and Case 2 is the correct one. Case 2 :: ? (N, ?, Y) : Mad Ade (?, ?, Y) : ? (N, ?, N) : Cliff Hedge (Y, Y, N) Again from (3) and (4), there are 2 possibilities as shown below. Case 2a :: Donny Moe (N, N, Y) : Mad Ade (?, N, Y) : Buster Artery (N, N, N) : Cliff Hedge (Y, Y, N) Case 2b :: Buster Artery (N, N, Y) : Mad Ade (?, Y, Y) : Donny Moe (N, N, N) : Cliff Hedge (Y, Y, N) Thus, Cliff Hedge is fair, handsome and unscarred. Also, Mad Ade may be either fair or not fair.	From (2), both the men standing next to Mad Ade are not fair. Also, exactly one man is fair, handsome and unscarred. Hence, there are two cases:	2.23	2.85	0D	H	5	4	4.9926	4	Traits	null	Cliff Hedge
49	Madadian Race Horses	Mad Ade's rich uncle "Uncle Rich" owned the famous Madadian Race horse breeding stables "The Gluepot". It has a private race track that has five lanes. Uncle Rich has 25 horses and wishes to know which are the three fastest. What is the least number of races needed to be run to find the answer? Note that it is only the ranking of the horses being found not the actual timings.	Answer: 7 races Race #1 to Race #5 - Divide the horses into 5 groups of 5. Race each group to rank the first 3 in each - that's 5 races. Race #6 - Race the winner from each group. The winner in this race is the fastest horse. Race #7 - Race the second and third horses from the race in which the fastest horse raced initially, the first and second horses from the group of the second horse in Race #6, and the third horse in Race #6 (that's a total of 5 horses). The first and second horses in Race #7 are the second and third horses of the entire stable.	Subgroups!	2.39	2.84	Algorithm	H	x	x	x	x	Measurement	null	7
50	5 Wood-cutting Machines	In a wood-cutting factory, five large sawing machines stand in a windowless room. Each machine has an on/off switch attached, there being no doubt as to which switch controls which machine. Outside the door to the room are five back-up on/off switches, one for each machine inside. The power for each machine must first pass through the back-up switch, and then the machine switch before reaching the saw. The problem is, the new manager cannot decide how these back-up switches match with the machines inside the room. One day, the manager's brother visits. The manager takes him inside the sawing room where all five machines are at work and explains the problem. The brother announces that he intends to leave the room and that when he returns he will be able to match correctly the five switches outside the room to the five machines inside. The brother works alone, cannot see the machines from outside the room and solves the problem purely by operating switches. How is it possible?	1) Turn off two machines while inside. Let's call those two machines turned off with inside switch 'inactive', and call remaining three machines 'active'. 2) Go outside. 3) Find out which two outside switches correspond to inactive machines, and which correspond to active machines. To do that, try all of following ten combinations, where 'x' represents turned-off outside switch, while 'O' represent turned on switch: xxx00,xx0x0,x0xx0,0xxx0,xx00x,x0x0x,0xx0x,x00xx,0x0xx,00xxx . Only one of these combinations is a 'silent' combination that eliminates all sound, by turning off all three active machines. 4) Label outside switches related to active machines (those marked with 'x' in the silent combination) with A, B, and C. Label outside switches related to inactive machines with D and E. 5) For inactive machines, turn D off and E on. 6) For active machines, turn A and B on, and turn C off. 7) Wait enough time for machine connected to C switch to cool off, and then turn B off, too. 8) Go inside. 9) The only machine that is still working inside is connected to outside switch A. 10) Check both machines that were active and are now turned off. The one that is warmer is connected to switch B (since it was on most recently), and the cooler one is connected to switch C (which was turned off first). 11) Turn inside switches on for both 'inactive' machines. The one that starts working is connected to outside switch E. The one that is still not working is connected to outside switch D.	Aside from sight, use other senses.	2.27	2.84	x	null	x	x	x	x	null	null	1) Turn off two machines while inside. Let's call those two machines turned off with inside switch 'inactive', and call remaining three machines 'active'. 2) Go outside. 3) Find out which two outside switches correspond to inactive machines, and which correspond to active machines. To do that, try all of following ten combinations, where 'x' represents turned-off outside switch, while 'O' represent turned on switch: xxx00,xx0x0,x0xx0,0xxx0,xx00x,x0x0x,0xx0x,x00xx,0x0xx,00xxx . Only one of these combinations is a 'silent' combination that eliminates all sound, by turning off all three active machines. 4) Label outside switches related to active machines (those marked with 'x' in the silent combination) with A, B, and C. Label outside switches related to inactive machines with D and E. 5) For inactive machines, turn D off and E on. 6) For active machines, turn A and B on, and turn C off. 7) Wait enough time for machine connected to C switch to cool off, and then turn B off, too. 8) Go inside. 9) The only machine that is still working inside is connected to outside switch A. 10) Check both machines that were active and are now turned off. The one that is warmer is connected to switch B (since it was on most recently), and the cooler one is connected to switch C (which was turned off first). 11) Turn inside switches on for both 'inactive' machines. The one that starts working is connected to outside switch E. The one that is still not working is connected to outside switch D.
51	Kebab Shop Line Up	There had been a break in at the "Sweaty Chef" Kebab shop, and the new owner, Mustapha Bettaname, had been robbed of his secret kebab recipe. The police had one eye witness, Al Kaholic, the local wino and world champion turps nudger. A Police line up of 11 suspects was made to stand in a straight line to have an Identity Parade. The main culprit was asked to stand in the center of the line-up. 1) Barb Dwyre and Chris Mass stood to the right of the main culprit 2) Two suspects stood between Ewan Watarmy and Lou Stooth 3) Seven suspects stood between Mike Rhosopht and Phil Mypokits 4) Gerry Atrick stood to the right of Hugo Phurst 5) Robin Banks and Polly Ester-Phants stood either side of Ewan Watarmy 6) Diddy Dewit and Polly Ester-Phants stood to the left of the main culprit 7) Six suspects stood between Chris Mass and Ewan Watarmy 8) Two suspects stood between Ewan Watarmy and Diddy Dewit Who is the main culprit?	Suspects from left to right: Diddy Dewit, (Mike Rhosopht/Phil Mypokits), (Robin Banks/Polly Ester-Phants), Ewan Watarmy, (Robin Banks/Polly Ester-Phants), HUGO PHURST, Lou Stooth, (Barb Dwyre/Gerry Atrick), (Barb Dwyre/Gerry Atrick), (Mike Rhosopht/Phil Mypokits), Chris Mass Let's number the positions 1 to 11 from left to right. Hence, the main culprit is at position 6. Now, looking at the clues 7, 5, 2 and 8 together: Position 1 - Diddy Dewit or Lou Stooth Position 3 - Polly Ester-Phants or Robin Banks Position 4 - Ewan Watarmy Position 5 - Polly Ester-Phants or Robin Banks Position 7 - Diddy Dewit or Lou Stooth Position 11 - Chris Mass From clue (3), the only possible positions for Mike Rhosopht and Phil Mypokits are Position 2 and Position 10. Now there are 3 positions remaining - 6, 8 and 9 and remaining 3 suspects are Hugo Phurst, Barb Dwyre and Gerry Atrick. But from clue (1), Barb Dwyre stood to the right of the main culprit i.e. Barb Dwyre must be on position 8 or 9 as position 6 is for the main culprit. So either Hugo Phurst or Gerry Atrick is the main culprit. From (4), Gerry Atrick stood to the right of Hugo Phurst. Hence, Hugo Phurst is the main culprit. Suspects from left to right are: Diddy Dewit, (Mike Rhosopht/Phil Mypokits), (Robin Banks/Polly Ester-Phants), Ewan Watarmy, (Robin Banks/Polly Ester-Phants), HUGO PHURST, Lou Stooth, (Barb Dwyre/Gerry Atrick), (Barb Dwyre/Gerry Atrick), (Mike Rhosopht/Phil Mypokits), Chris Mass. Thus, Diddy Dewit (1), Ewan Watarmy (4), Hugo Phurst (6), Lou Stooth (7) and Chris Mass (11) are the suspects whose positions are fixed. Mike Rhosopht and Phil Mypokits are at position 2 or 10. Robin Banks and Polly Ester-Phants are at position 3 or 5. Barb Dwyre and Gerry Atrick are at position 8 or 9.	Start with clues 7, 5, 2 and 8 together	2.21	2.84	1D	H	2	11	7.6012	8	null	null	HUGO PHURST
52	The Eight Queens	One of the most famous logic puzzles is the "Eight Queens puzzle". The object of this puzzle is to place 8 chess queens on a standard 8x8 chessboard so that no queen can be captured by any of the other queens. Logically, no queen can share the same row, column, or diagonal with any other queen. Can you discover an arrangement that works?	There are actually 12 completely unique solutions to this puzzle (unique meaning not simply rotating or flipping the board). Using a standard system of numbering rows 1-8 moving away from the player and noting columns with letters a-h, here are the solutions: 1) a1, g2, e3, h4, b5, d6, f7, c8 2) a1, g2, d3, f4, h5, b6, e7, c8 3) c1, a2, g3, e4, h5, b6, d7, f8 4) d1, a2, e3, h4, b5, g6, c7, f8 5) e1, a2, h3, d4, b5, g6, c7, f8 6) e1, a2, d3, f4, h5, b6, g7, c8 7) e1, a2, h3, f4, c5, g6, b7, d8 8) e1, c2, a3, g4, b5, h6, f7, d8 9) e1, g2, a3, d4, b5, h6, f7, c8 10) f1, a2, e3, b4, h5, c6, g7, d8 11) f1, c2, a3, h4, d5, b6, g7, e8 12) g1, a2, c3, h4, f5, d6, b7, e8	Queens placed, separated like knights, cannot see each other.	2.13	2.84	2D	null	2	64	9.646	1	null	null	Any of these possible solutions: 1) a1, g2, e3, h4, b5, d6, f7, c8 2) a1, g2, d3, f4, h5, b6, e7, c8 3) c1, a2, g3, e4, h5, b6, d7, f8 4) d1, a2, e3, h4, b5, g6, c7, f8 5) e1, a2, h3, d4, b5, g6, c7, f8 6) e1, a2, d3, f4, h5, b6, g7, c8 7) e1, a2, h3, f4, c5, g6, b7, d8 8) e1, c2, a3, g4, b5, h6, f7, d8 9) e1, g2, a3, d4, b5, h6, f7, c8 10) f1, a2, e3, b4, h5, c6, g7, d8 11) f1, c2, a3, h4, d5, b6, g7, e8 12) g1, a2, c3, h4, f5, d6, b7, e8

End of preview.

The Brainteaser dataset

This is a dataset concurrently released with our paper:

Creativity or Brute Force? Using Brainteasers as a Window into the Problem-Solving Abilities of Large Language Models [PDF]

Citation

If you use this dataset, please cite our paper:

@article{han2025creativity,
  title={Creativity or Brute Force? Using Brainteasers as a Window into the Problem-Solving Abilities of Large Language Models},
  author={Han, Simeng and Xia, Stephen and Zhang, Grant and Dai, Howard and Liu, Chen and Chen, Lichang and Nguyen, Hoang Huy and Mei, Hongyuan and Mao, Jiayuan and McCoy, R. Thomas},
  journal={arXiv preprint arXiv:2505.10844},
  year={2025}
}

Highlights

We introduce a novel benchmark dataset, BRAINTEASER, which uses brainteasers to evaluate the reasoning abilities of LLMs.
The Math and Logic datasets were curated by scraping problem-solving and reasoning questions from the Braingle website, an online platform of puzzles and brain teasers.
Authored by expert problem solvers, BRAINTEASER features diverse puzzle styles and complexities, aiming to isolate models’ reasoning abilities rather than their memorization of formulas.
BRAINTEASER is exclusively centered on mathematical and logical puzzles, all authored by expert problem solvers with demonstrated proficiency across a wide range of puzzle types.
As quality control, we conducted one round of manual inspection of all problems in BRAINTEASER done by college students who belong to a math club; these students have extensive experience in solving competition-level math problems.
During manual inspection, low-quality and ambiguously described problems were removed, leaving 242 Math and 236 Logic problems in the dataset. The same annotators also manually created hints for problems that originally lacked them.
The same annotators assigned cateogries and subcategories to all puzzles (see Table 1).

Dataset composition

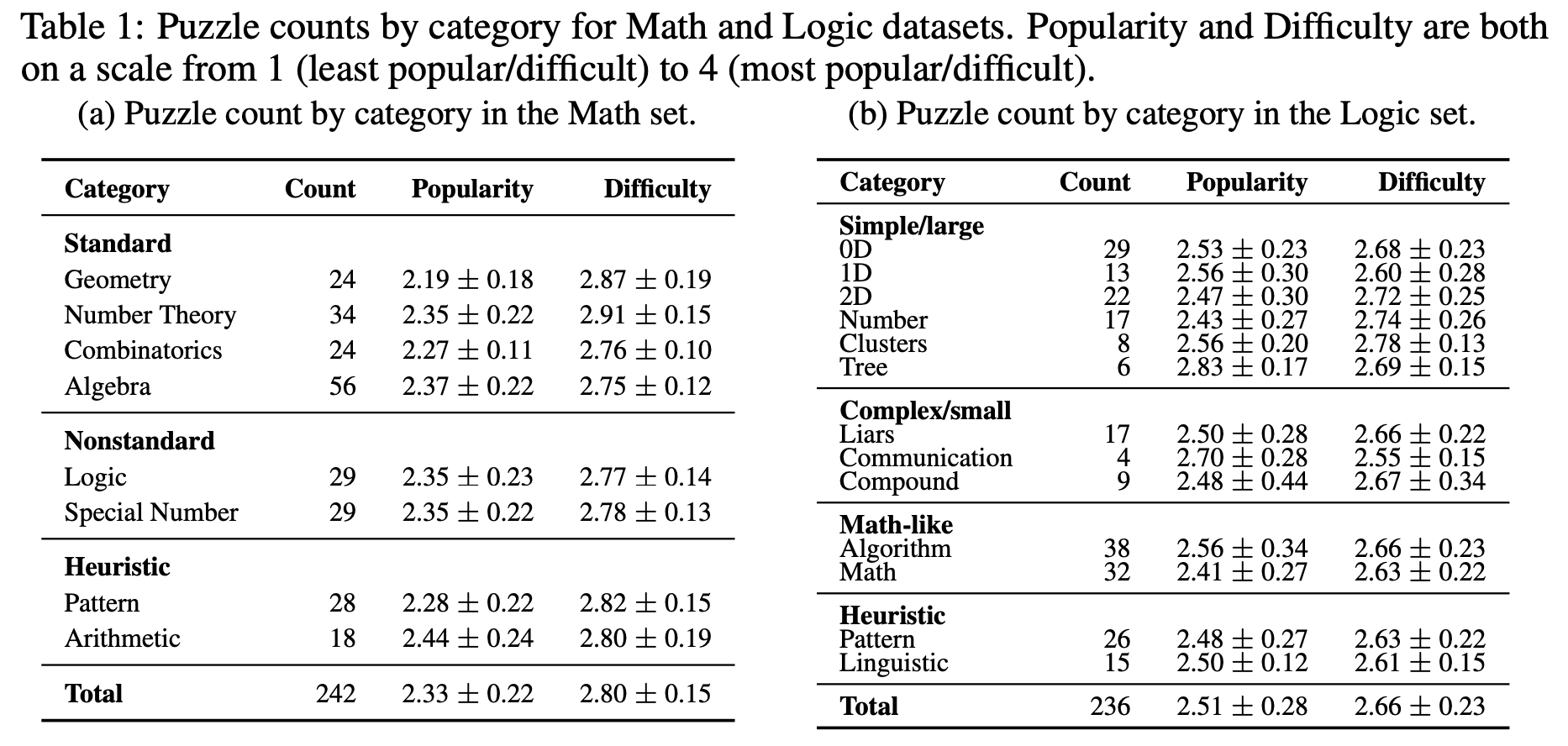
Main observations

Creativity vs. Brute Force

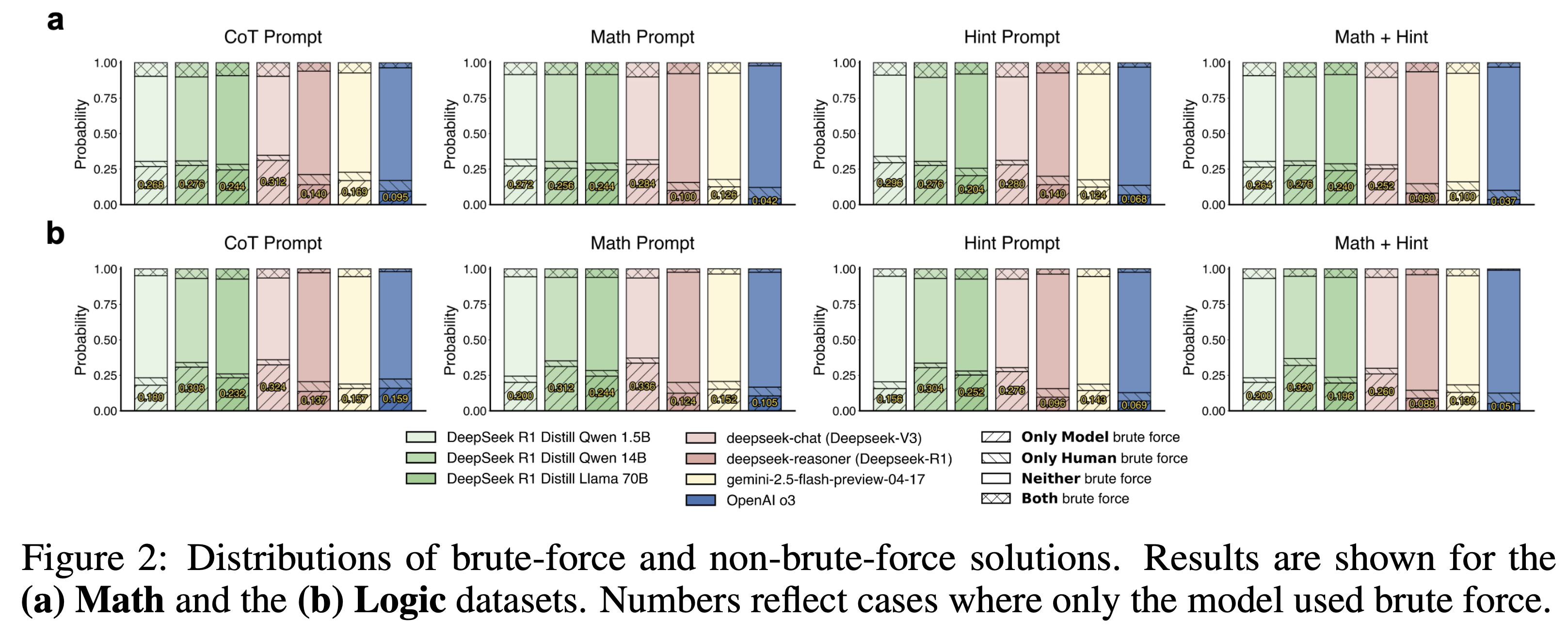
Downloads last month: 35